Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

По смыслу задачи k > 1, p > 0. Следовательно, подкоренное выражение будет неотрицательным, если k ≤ 2, т. е. 1 < k ≤ 2.

Так как

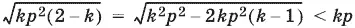
(мы знаем, что k > 1), то оба значения x неотрицательны. Легко проверить, что p − x 1= x 2.

Ответ.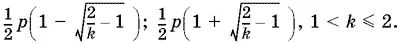

18.7.Примем расстояние, которое туристам нужно пройти на моторной лодке, за единицу. Через x кг/ч обозначим расход горючего в течение часа работы двигателя в режиме, обеспечивающем собственную скорость лодки v 1, а через y кг/ч — расход горючего при работе двигателя во втором режиме ( v 2). Весь путь лодка пройдет за ч при работе двигателя в первом и во втором режимах соответственно. Так как расход горючего будет одинаковым, то

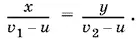
Если скорость течения реки будет равна ku , то из условия получим второе уравнение

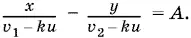
Найдя из первого уравнения x , подставим во второе. Получим

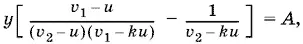
откуда

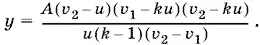
Так как k > 1, то y > 0 только при v 2> v 1и ku < v 1. Общий расход горючего равен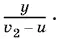

Ответ.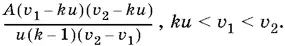

18.8.Обозначим через x , y , z , s и t количество десятков порций стоимостью по 7, 9, 11, 13 и 15 p. за порцию соответственно.

Условия задачи можно переписать в виде системы

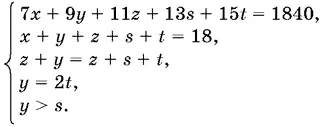
Вычитая из первого уравнения второе, умноженное на 7, получим

y + 2 z + 3 s + 4 t = 29

или (так как y = 2 t )

2 z + 3 s + 6 t = 29.

В результате сравнения второго и третьего уравнений найдем

z + s + t = 9.

Умножим это уравнение на два и вычтем из предыдущего уравнения:

s + 4 t = 11.

Поскольку s и t — натуральные, t может принимать лишь два значения: t = 1 и t = 2, иначе уравнение s + 4 t = 11 не выполняется. Если t = 1, то s = 7, а y = 2. Это противоречит требованию y > s . Следовательно, t = 2, s = 3, y = 4. Нетрудно найти, что x = 5, z = 4.

Ответ.50 порций мороженого по 7 p., 40 порций по 9 p., 40 порций по 11 p., 30 порций по 13 p., 20 порций по 15 p.

18.9.Обозначим время, за которое плоты прошли путь по озеру, через x . Так как весь путь они прошли за 11,5 суток, т. е. за 276 ч, то путь AC (буквой С обозначено устье реки) — за 276 − x ч, а скорость течения реки равна AC / 276 − x .

Выразим скорость течения реки с помощью остальных условий задачи. Если пароход проходит путь от А до В за 40 ч, а путь от С до В за x ч (идет в два раза быстрее, чем с плотами), то скорость парохода вниз по течению реки равна 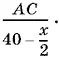Аналогично его скорость вверх по течению равна 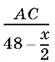. Если вычесть из первой скорости вторую, то получим удвоенную скорость течения реки. Мы пришли к уравнению

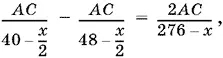
решая которое найдем: x 1= 24, x 2= 136. Второй корень посторонний, так как 40 − x / 2и 48 − x / 2становятся отрицательными, что не имеет физического смысла.

Ответ.24 ч.

18.10.Пусть v 1, v 2и v 3— скорости пловцов, а x − расстояние AC (рис. P.18.10).

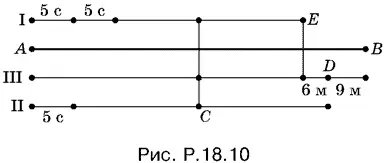
Приравниваем времена, за которые пловцы проплыли путь AC :

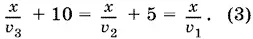
Из условия встречи в точке D третьего и второго пловцов получим

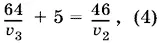
а из условия встречи в точке E третьего и первого:

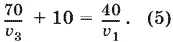
Так как в уравнение (4) входят v 2и v 3, а в уравнение (5) v 1и v 3, то уравнения (3) перепишем в виде

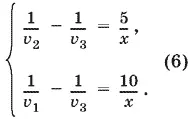
Преобразуем теперь уравнения (4) и (5):

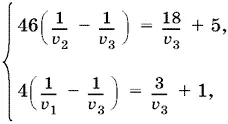
и воспользуемся заменой (6). Получим систему

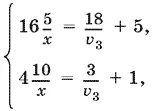
из которой проще исключить v 3. Найдем x = 10. Следовательно, v 3= 1.

Ответ.1 м/с.

18.11.Обозначим через x часть сосуда, занимаемую раствором кислоты, а объем всего сосуда примем за единицу. После того как сосуд долили q %−м раствором, количество концентрированной кислоты стало

px / 100+ q (1 − x )/ 100,

а новая концентрация

p 1= px + q (1 − x ) = ( p − q ) x + q .

Если вместо p подставить р 1, то получим р 2, аналогично можно получить р 3и т. д. Приходим к рекуррентному соотношению

р k = x(р k − 1− q ) + q .

Вычислим р 2:

р 2= x ( р 1− q ) + q = х ²( p − q ) + q .

По индукции легко доказать, что

р k = x k ( p − q ) + q .

Так как p k = r , то получим уравнение

r = x k ( p − q ) + q ,

откуда

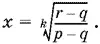
Ответ. 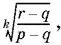где либо r > q , p > q , либо r < q , p < q .