Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

18.12.Пусть x и y — скорости автомобиля и мотоцикла соответственно, а z — длина пути AB . Тогда первая встреча произойдет через z / x + y ч после начала движения на расстоянии zy / x + y от пункта В . Те же рассуждения, примененные к отрезку длиной в zy / x + y , позволят найти расстояние между первым и вторым пунктами встречи. По условию это расстояние равно 2 z / 9, т. е.

zyx / ( x + y )²= 2/ 9 z , или yx / ( x + y )²= 2/ 9.

Это уравнение можно переписать так:

2 x ² − 5 ху + 2 y ² = 0, т. е. 2( x / y )² − 5 x / y + 2 = 0,

откуда

либо x / y = 2, либо x / y = ½. (7)

Очевидно, что эти отношения дают симметричные решения. Если предположить, что скорость автомобиля больше скорости мотоцикла, то x = 2 y .

Используем оставшиеся условия задачи. Если бы скорость автомобиля была на 20 км/ч меньше, т. е. равнялась бы ( x − 20) км/ч, то первая встреча произошла бы через 3 ч после начала движения. Получаем уравнение

z / x + y − 20= 3. (8)

Мотоцикл до встречи преодолел бы в этом случае расстояние в 3 y км, а расстояние между пунктами первой и второй встреч составило бы 3 yx / x + y − 20. Получаем третье уравнение:

3 y ( x − 20)/ x + y − 20= 60. (9)

Подставим в это уравнение x = 2 y . Получим квадратное уравнение, корнями которого являются

y 1= 20 + 10√2, y 2= 20 − 10√2.

Второе значение не подходит, так как тогда x 2< 20.

Итак,

y = (20 + 10√2) км/ч, x = (40 + 20√2) км/ч,

а из уравнения (8) найдем z = (120 + 90√2) км.

Ответ.(120 + 90√2) км.

18.13. Пусть пассажир опоздал на поезд на t ч, проехал на такси x км, а на автобусе y км. Скорость поезда обозначим через u . Тогда путь до встречи с поездом пассажир проедет за 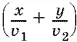ч, а поезд пройдет этот путь за x + y / u ч. Учтя опоздание пассажира, получим

Поездка на такси и автобусе обошлась пассажиру в ( ax + А ) p. Если бы он ехал все время на такси, то это стоило бы ( ax + А − В ) p. и он догнал бы поезд, проехав ax + А − В / a км. Приравнивая времена, за которые этот путь прошел поезд и проехал догонявший его пассажир, получим второе уравнение:

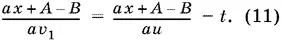
Третье уравнение очевидно:

Записав его в виде

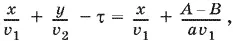
найдем

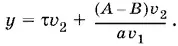
Приравниваем выражения для t из уравнений (10) и (11). Получим

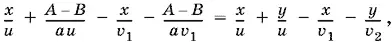
т. е.

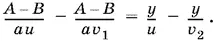
Поскольку y уже найден, можно вычислить u :

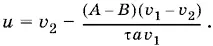
Чтобы задача имела решение, скорость поезда должна быть положительной. Так как v 1> v 2и А > В , то из неравенства

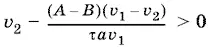
следует, что

Ответ.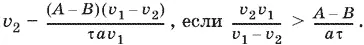

18.14.Обозначим скорость товарного поезда до остановки через x , расстояние AB через y , а расстояние AC через z . Тогда пассажирский поезд шел вначале со скоростью mx , а после остановки оба поезда шли соответственно со скоростями 5 x / 4и 5 mx / 4. Весь путь без остановки товарный поезд прошел бы за y / x ч. Поскольку он сделал остановку на t ч в z км от А, а затем прошел оставшиеся ( y − z ) км со скоростью 5 x / 4, то он прошел весь путь за

z / x + 4( y − z )/ 5 x + t ч.

Следовательно,

y / x + t 1= z / x + 4( y − z )/ 5 x + t .

Аналогичное уравнение составляем для пассажирского поезда, который шел в обратном направлении:

y / mx + t 2= y − z / mx + 4 y / 5 mx + t .

Чтобы ответить на вопрос задачи, нужно из времени, за которое товарный поезд прошел отрезок AC , вычесть время, за которое пассажирский поезд прошел расстояние BC . В наших обозначениях эта разность запишется так:

z / x − y − z / mx .

Именно это выражение нам нужно определить с помощью полученных выше уравнений. Мы может добиться этого, решив уравнения относительно z / x и y / x . После простых преобразований система примет вид

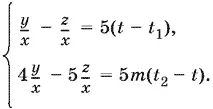
Умножив первое уравнение на −4 и сложив со вторым, найдем z / x , а умножив его на −5 и сложив со вторым, найдем y / x :

y / x = 25( t − t 1) − 5 m ( t 2− t ), z / x = 20( t − t 1) − 5 m ( t 2− t ).

Остается подставить найденные значения в выражение

( m + 1) z / mx − y / mx .

Ответ. 5/ m [(4 m − 1)( t − t 1) − m ²( t 2− t )].

18.15.Обозначим скорость самолета через x , а скорость вертолета через y . До первой встречи вертолет летел d / y ч, а самолет — d / x ч. Так как самолет вылетел на t ч позднее, то

d / y = d / x + t .

Второе уравнение мы получим из условия второй встречи. Вертолет к этому моменту находился в d км от В и пробыл в полете s − d / y ч. Самолет, преодолев расстояние s + d , пробыл в полете s + d / x ч. Следовательно,

s − d / y = s + d / x + t .

Хотя полученную систему уравнений можно решить, а затем ответить на вопрос задачи, мы сначала вычислим интересующую нас величину в предположении, что x и y известны. Вертолет прилетел в В через s / y ч после вылета. Самолет вернулся в А через ( t + 2 s / x ) ч после того, как вертолет вылетел из А . Нас интересует величина