Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Требование, чтобы числа x + 1, хq + 2, хq ² + 1 образовывали арифметическую прогрессию при таком решении, оказывается лишним.

Ответ.842.

19.13.Пусть в колхозе было n комбайнов, один смог бы убрать весь урожай за x ч непрерывной работы, а при работе по плану все комбайны одновременно находились в поле y ч. Так как все комбайны могут справиться с уборкой за 24 ч, а производительность одного комбайна 1/ x , то

24/ xn = 1, т. е. 24 n = x .

Если комбайны работают по плану, то, работая вместе, они сделали п 1/ x y часть всей работы. Кроме этого, первый комбайн работал n − 1 ч, второй n − 2, а ( n − 1)−й работал один час. Учитывая все это, получим уравнение

n − 1/ x + n − 2/ x + ... + 1/ x + n 1/ xy = 1,

или

n − 1/ 2 n + ny = x .

Так как x = 24 n , то из этого уравнения можно выразить y через n :

y = 24 − n − 1/ 2.

Наконец, последнее условие задачи можно записать в виде уравнения

( n + y − 7)( n − 5) 1/ x = 1.

Подставляя вместо x и y их выражения через n , придем к квадратному уравнению

( n + 17 − n − 1/ 2)( n − 5) = 242 n ,

т. е. n ² − 18 n − 175 = 0.

Решая это уравнение, найдем n 1= 25, n 2= −7. Второй корень не имеет смысла.

Ответ.25.

19.14.Пусть братьям a , aq и aq ² лет. Тогда они получат соответственно x , xq и xq ² p.

Через 3 года им будет a + 3, aq + 3 и aq ² + 3 лет, причем старшему окажется вдвое больше лет, чем младшему:

aq ² + 3 = 2( a + 3). (1)

При дележе через 3 года младший брат получит x + 105, средний xq + 15. Чтобы узнать, сколько получит старший брат, вычтем эти деньги из всей суммы:

x + xq + xq ² − ( x + 105) − ( xq + 15) = xq ² − 120.

Так как братья делят деньги пропорционально их возрасту, то получим еще два уравнения:

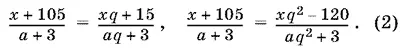
Уравнение (1) позволяет записать второе из уравнений (2) так:

2( x + 105) = xq ² − 120,

т. е.

x ( q ² − 2) = 330. (3)

Если в (1) раскрыть скобки, а затем вынести за скобки a , то

a ( q ² − 2) = 3. (1′)

Сравним с уравнением (3):

x = 110 a .

Первое из уравнений (2) можно переписать так:

(110 a + 105)( aq + 3) = (110 aq + 15)( a + 3), т. е. 5 aq − 7 a = 6.

Решим его совместно с уравнением (1′):

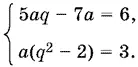
Из первого уравнения а = 6/ 5 q − 7. Подставим во второе. После преобразований получим квадратное уравнение

6 q ² − 15 q + 9 = 0,

откуда q 1= 3/ 2, q 2= 1.

Второй корень посторонний, так как тогда всем братьям одинаковое количество лет и никто из них не может через 3 года стать вдвое старше другого.

Ответ.12, 18, 27.

19.15.Пусть а , b , с и а ², b ², с ². Другими словами, 2 b = а + с и b 4= а ² с ². Если первое уравнение возвести в квадрат

4 b ² = а ² + 2 aс + с ²,

а второе записать в виде b ² = | ac |, то, сравнивая левые части этих равенств, найдем

а ² + 2 aс + с ² = 4| ac |.

Если а и с одного знака, получаем уравнение

а ² − 2 aс + с ² = 0, т. е. ( а − с )² = 0,

откуда а = с . Следовательно, а ² = с ² и знаменатель прогрессии а ², b ², с ² равен 1. Если а и с разных знаков, получаем уравнение

а ² + 6 ас + с ² = 0.

Разделим на а ² (по условию а ≠ 0) и решим уравнение

( c / a )² + 6 c / a + 1 = о

относительно c / a :

c / a = −3 ± √8.

Так как c ²/ a ²= q ², то

q ² = (−3 ± √8)².

Числа а ², b ² и с ², образующие геометрическую прогрессию, положительны. Следовательно, q > 0. Таким образом, из последнего уравнения

q 2,3= 3 + √8.

Ответ.3 − √8; 1; −3 + √8.

19.16.При n = 1 формулы верны:

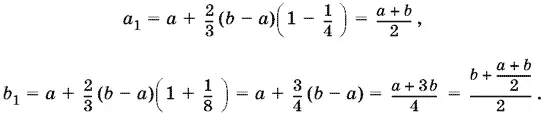
Предположим, что эти формулы верны для n = k, и докажем, что они верны для n = k + 1:

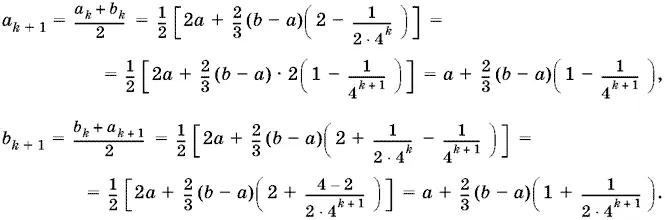
Так как 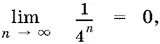то предел последовательности равен a + ⅔( b − a ) = a + 2 b / 3.

Ответ. a + 2 b / 3.

19.17.Данное уравнение равносильно совокупности двух уравнений

(8 a − 3) x + (14 a + 5) x = 2 k π, (14 a + 5) x − (8 a − 3) x = 2 n π,

или

(11 a + 1) x = k π, (3 a + 4) x = n π.

Так как по условию a > 0, то 11 a + 1 ≠ 0 и 3 a + 4 ≠ 0. Поэтому

x k = k π/ 11 a + 1, x n = n π/ 3 a + 4.

Значения x k и x n при k , n = 0, 1, 2, ... (по условию x ≥ 0) образуют две прогрессии с разностями

d 1 = π/ 11 a + 1, d 2= π/ 3 a + 4

и первыми членами, равными нулю. Числа x k и x n , расположенные в порядке возрастания, составляют арифметическую прогрессию тогда и только тогда, когда их разности кратны, т. е. либо d 2= d 1 m при d 1 ≤ d 2, либо d 1 = d 2 m при d 2 ≤ d 1( m — натуральное число). Пусть, например, d 1 ≤ d 2. Тогда d 1— второй член новой прогрессии (первый ее член равен нулю) и d 1— разность этой прогрессии. Однако число d 2, являясь членом второй прогрессии, также должно войти в новую прогрессию. Поэтому d 2 = 0 + d 1 m = d 1 m . Обратно, если d 2 = d 1 m и d 1 ≤ d 2, то x n = d 2 n = d 1 mn , т. е. каждый член второй прогрессии является членом первой прогрессии. Аналогичное доказательство может быть проведено для случая d 2 ≤ d 1.

Итак, для d 1≤ d 2 имеем

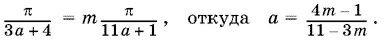
Так как m — натуральное, то 4 m − 1 > 0. В свою очередь а > 0, а потому 11 − 3 m > 0 и m < 11/ 3. Получаем три возможных значения m — 1, 2, 3 и соответствующие им значения а = 3/ 8, 7/ 5, 11/ 2.

Для d 2 ≤ d 1получим

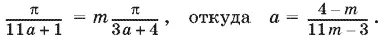
При натуральном m разность 11 m − 3 положительна, а так как а > 0, то 4 − m > 0 или m < 4. Каждому из трех возможных значений m = 1, 2, 3 будет соответствовать свое значение а = 3/ 8, 2/ 19, 1/ 30.