Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ. 1/ 30, 2/ 19, 3/ 8, 7/ 5, 11/ 2.

20.1.Докажем, что

S = ½ + ... + 1/ n ²< 1.

Так как

1/ (1 + k )²< 1/ k (1 + k ),

то

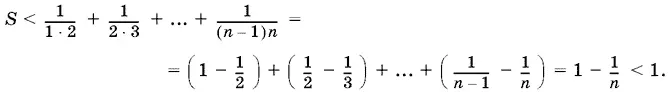
При доказательстве мы воспользовались тем, что

1/ ( n − 1) n = 1/ n − 1− 1/ n .

Такой прием часто применяется и называется разложением дроби на простейшие .

20.2.Так как

то

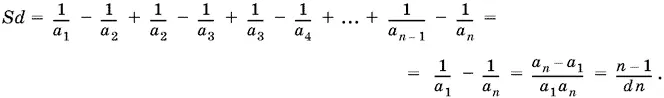
Ответ. n − 1/ d ² n .

20.3.Представим k −e слагаемое в виде

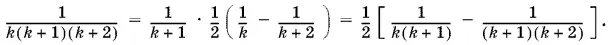
Тогда

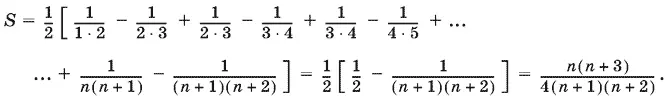
Ответ.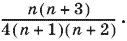

20.4.Левую часть данного равенства перепишем в виде

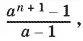
воспользовавшись для этого формулой суммы членов геометрической прогрессии. Тогда (поскольку а ≠ 1)

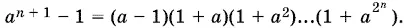
Правая часть может быть записана так:

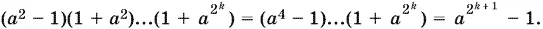
Итак,

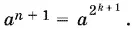
По условию а ≠ 0, 1, −1. Это позволяет найти нужную нам зависимость.

Ответ. n + 1 = 2 k + 1.

20.5.Расположим коэффициенты данного многочлена слева направо и разместим под ними коэффициенты того же многочлена, расположенные в обратном порядке,

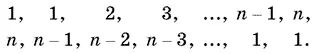
Теперь можно выписать коэффициент при x n , составив сумму попарных произведений расположенных один под другим множителей:

1 · n + 1( n − 1) + 2( n − 2) + 3( n − 3) + ... + ( n − 1)1 + n · 1.

Эту сумму можно преобразовать так:

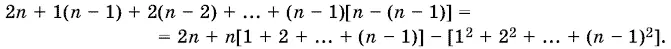
Каждую из сумм, стоящих в скобках, легко подсчитать:

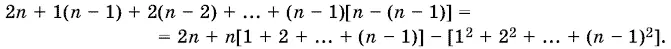
Таким образом, искомый коэффициент равен

Ответ.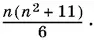

20.6.Неравенство равносильно системе (в левой его части — абсолютная величина суммы членов бесконечно убывающей геометрической прогрессии со знаменателем — 2 x ):

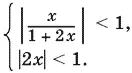
Из второго неравенства следует, что −1 < 2 x < 1, т. е. 1 + 2 x > 0. Поэтому первое неравенство можно переписать в виде

| x |/ 1 + 2 x < 1, или | x | < 1 + 2 x .

Таким образом, приходим к системе

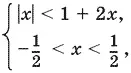
которая равносильна совокупности двух систем

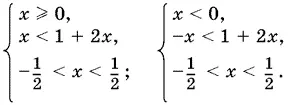
Ответ.−⅓ < x < ½.

20.7.Так как k · k ! = ( k + 1)! − k !, то

2! − 1! + 3! − 2! + 4! − 3! + ... + ( n + 1)! − n ! = ( n + 1)! − 1.

Ответ.( n + 1)! − 1.

20.8.Домножим S n на x ²:

x ² S n = x ³ + 4 x 5+ 7 x 7+ ... + (3 n − 2) x 2 n + 1,

и вычтем полученное выражение из S n :

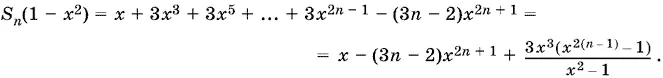
Ответ.

20.9.Рассмотрим тождество [22] Формулы для и т. п. доказываются аналогично с помощью тождеств: ( x + 1)³ = x ³ + 3 x ² + 3 x + 1, ( x + 1) 4 = x 4 + 4 x ³ + 6 x ² + 4 x + 1.

( x + 1) 5= x 5+ 5 x 4+ 10 x ³ + 10 x ² + 5 x + 1.

Положим в нем последовательно x = 1, 2, ..., n и сложим n полученных равенств:

2 5+ 3 5+ ... + ( n + 1) 5= 1 + 2 5+ 3 5+ .. + n 5+ 5(1 4+ 2 4+ ... + n 4) + 10(1³ + 2³ + ... + n ³) + 10(1² + 2² + ... + n ²) + 5(1 + 2 + ... + n ) + n .

После приведения подобных получим

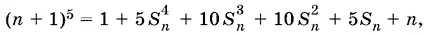
откуда

Так как

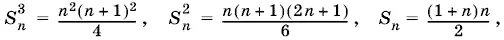
то

Многочлен третьей степени, стоящий в скобках, имеет корень n = −2 и поэтому делится на 2n + 1.

Ответ. 1/ 30 n ( n + 1)(2 n + 1)(3 n ² + 3 n − 1).

20.10.В n −й группе содержится n членов.

Пусть n четное. Подсчитаем число четных чисел, встречающихся во всех группах до n− й. Это число равно

2 + 4 + 6 + ... + ( n − 2) = n ( n − 2)/ 4.

Следовательно, последнее четное число, встречающееся до n −й группы, равно 2 n ( n − 2)/ 4 = n ( n − 2)/ 2, а первое четное число, входящее в n −ю группу, равно n ( n − 2)/ 2+ 2. Теперь можно найти сумму n последовательных четных чисел, начинающихся с n ( n − 2)/ 2+ 2. Эта сумма равна

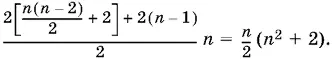
Пусть теперь n четное. Число нечетных членов, встречающихся до n −й группы, равно

1 + 3 + 5 + ... + ( n − 2) = ( n − 1)²/ 4.

Последним нечетным числом, стоящим до n −й группы, будет ( n − 1)²/ 2− 1, а первым числом, входящим в n −ю группу, — число ( n − 1)²/ 2+ 1. Следовательно, сумма n последовательных нечетных чисел, начиная с ( n − 1)²/ 2+ 1, равна