Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Делаем проверку иррационального уравнения.

Ответ.±1, 0.

22.10.Из условия следует, что x > 0. В таком случае

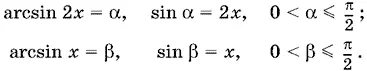
Уравнение примет вид α + β = π/ 3, и обе его части окажутся в интервале (0, π], который является интервалом монотонности косинуса. Следовательно, уравнение

cos (α + β) = cos π/ 3

равносильно данному. Раскрывая скобки и заменяя тригонометрические функции α и β их выражениями через x , придем к уравнению

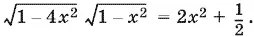
После возведения в квадрат получим

4(1 − 4 x ²)(1 − x ²) = (4 x ² + 1)².

При переходе к последнему уравнению могут появиться посторонние корни из−за того, что обе левые скобки могут стать отрицательными. Чтобы избежать этого, добавим условие |2 x | ≤ 1.

Уравнение 28 х ² − 3 = 0, к которому сводится последнее, имеет корни 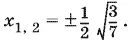Из них следует выбрать первый, так как он положителен и так как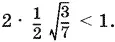

Ответ.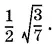

22.11.Обозначим

arctg (2 + cos x ) = α, arctg (2 cos² x / 2) = β.

Так как 2 + cos x > 0 и 2 cos² x / 2> 0, то 0 < α < π/ 2и 0 ≤ β < π/ 2.

Уравнение принимает вид α − β = π/ 4, причем

− π/ 2< α − β < π/ 2и − π/ 2< π/ 4< π/ 2.

Так как (− π/ 2, π/ 2) — интервал монотонности тангенса, то уравнение α − β = π/ 4равносильно уравнению tg (α − β) = tg π/ 4.

Переходя к уравнению

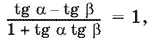
мы можем потерять те корни, для которых tg α или tg β не существует. В нашем случае этого не произойдет, поскольку

tg α = 2 + cos x , tg β = 2 cos² x / 2,

а правые части существуют всегда. Получаем уравнение

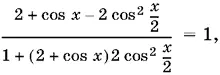
которое после преобразований принимает вид

2 cos 4 x / 2+ cos² x / 2= 0.

Так как уравнение 2 cos² x + 1 = 0 не имеет решений, то остается cos x = 0.

Ответ.π(2 n + 1).

22.12.Пусть

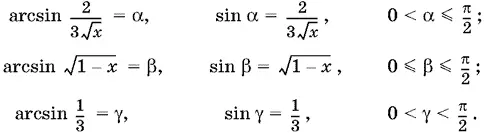
Так как − π/ 2< α − β ≤ π/ 2, то обе части уравнения лежат в интервале монотонности синуса. Поэтому уравнение равносильно такому:

sin (α − β) = sin γ

или

После упрощений получим уравнение

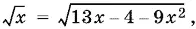
имеющее единственный корень x = ⅔. Делаем проверку и убеждаемся, что x = ⅔ является корнем предыдущего уравнения и, следовательно, корнем исходного уравнения.

Ответ.⅔.

22.13.Введем обозначения

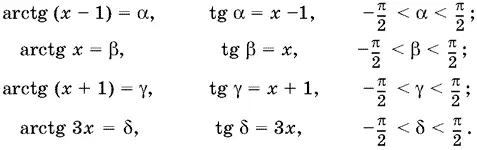
Наше уравнение принимает вид α + β + γ = δ или α + β = δ − γ. Обе части уравнения лежат в интервале (−π, π). Если мы возьмем котангенсы от обеих частей уравнения, то можем потерять лишь корень, которому соответствует значение углов, равное 0, так как это — единственное значение из интервала (−π, π), в котором котангенс не существует. Проверим, будет ли выполняться равенство α + β = δ − γ = 0. Если α + β = 0, то arctg (1 − x ) = arctg x , откуда 1 − x = x и x = ½. При x = 1 получим, что δ − γ = arctg 3/ 2− arctg 3/ 2= 0. Таким образом, x 1= ½ — корень уравнения. Если α + β ≠ 0, то от обеих частей уравнения можно взять котангенсы:

ctg (α + β) = ctg (δ − γ),

что приведет к следствию исходного уравнения. Раскрыв скобки и подставив выражения тригонометрических функций α, β, γ и δ через x , получим уравнение

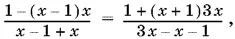
которое равносильно системе

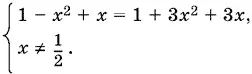
Получаем два значения неизвестного: x 2= 0, x 3= −½. Проверкой убеждаемся, что оба значения удовлетворяют данному уравнению.

Ответ.0, ±½.

23.1.С одной стороны, log 3sin x ≤ 0, так как sin x ≤ 1, а с другой стороны, log 3sin x ≥ 0, так как это выражение стоит под знаком квадратного корня. Остается единственная возможность:

log 3sin x = 0, sin x = 1, x = π(4 n + 1)/ 2.

Ответ. π(4 n + 1)/ 2.

23.2.Чтобы найти область определения данной функции, нужно решить систему

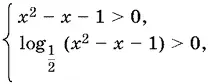
которая эквивалентна неравенству

0 < x ² − x − 1 < 1, или ( х ² − x − 1)( х ² − x − 2) < 0,

т. е.

( x − 1 − √5/ 2)( x − 1 + √5/ 2)( x + 1)( x − 2) < 0.

Ответ.−1 < x < 1 − √5/ 2; 1 + √5/ 2< x < 2.

23.3.Данное выражение принимает действительные значения, если x удовлетворяет неравенству

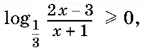
которое равносильно неравенству

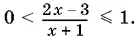
Его можно заменить системой

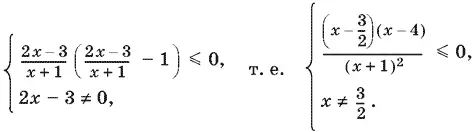
Ответ. 3/ 2< x ≤ 4.

23.4.Чтобы существовал арккосинус, необходимо и достаточно, чтобы

−1 ≤ x ² − З х + 1 ≤ 1,

т. е.

( х ² − З х + 2)( х ² − З х ) ≤ 0, или x ( x − 1)( x − 2)( x − 3) ≤ 0,

откуда

0 ≤ x ≤ 1, 2 ≤ x ≤ 3.

Из найденных интервалов нужно исключить точки, в которых tg 2 x не существует, т. е. числа x = π(2 n + 1)/ 4. Два из этих чисел: x = π/ 4и x = 3π/ 4лежат в найденных интервалах.

Ответ. 0 ≤ x < π/ 4, π/ 4< x ≤ 1, 2 < x < 3π/ 4, 3π/ 4< x ≤ 3.

23.5.Данное выражение принимает действительные значения, если удовлетворяется система неравенств

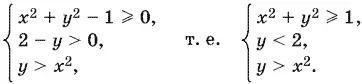
Решением этой системы будет часть плоскости, лежащая внутри параболы y = x ², вне круга x ² + y ² = 1 и ниже прямой y = 2, причем точки, лежащие на границе и принадлежащие или прямой, или параболе, не входят в область, а точки, лежащие на окружности (кроме точек А и С — рис. P.23.5), входят в область определения.