Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

23.6. Способ 1.Пусть Т — период функции. Тогда

cos ( x + Т )² = cos x ²

при всех x . Если x = 0, то получим cos Т ² = 1, откуда Т ² = 2 n π. Если x = Т √2 , то cos (√2 + 1)² Т ² = cos 2 Т ², откуда или

(√2 + 1)² Т ² + 2 Т ² = 2 k π, или (√2 + 1)² Т ² − 2 Т ² = 2 m π,

т. е.

либо (2 + 2√2) Т ² = 2 k π, либо (1 + 2√2) Т ² = 2 m π.

Подставляя в оба выражения Т ² = 2 n π, получим соответственно

5 + 2√2 = k / n или 1 + 2√2 = m / n ,

что невозможно, так как слева стоят иррациональные числа, а справа — рациональные.

Способ 2.Найдем корни функции cos x ²:

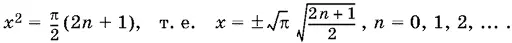
Рассмотрим положительные корни

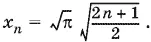
Предположим, что Т > 0 — период функции. Тогда, если при x = х 1функция равна нулю, то и при x = x 1+ Т она тоже равна нулю. Другими словами, х 1+ Т = x m . Аналогично x 2+ Т = х k . Вычитая одно равенство из другого, получим

т. е.

Возведем в квадрат:

После вторичного возведения в квадрат получим

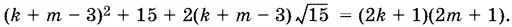
Это равенство возможно лишь при 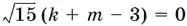, так как все остальные его элементы — целые. Однако числа k и m выбраны так, что k ≥ 3 и m ≥ 2, т. е. k + m > 3.

23.7.Если f ( x ) — периодическая функция с периодом Т , то при всех x должно выполняться тождество

sin ( x + Т ) + cos [ а ( x + Т )] = sin x + cos аx .

Положив в этом тождестве x = 0, x = − Т и x = Т , получим

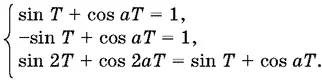
Из первого и второго равенств найдем cos aT = 1 и T = 2 n π/ a . Подставим найденное значение Т в последнее уравнение:

sin 4 n π/ a + cos 4 n π = sin 2 n π/ a + cos 2 n π,

т. е.

sin 4 n π/ a = sin 2 n π/ a ,

откуда или 4 n π/ a − 2 n π/ a = 2 k π, или 4 n π/ a + 2 n π/ a = (2 k + 1)π, т. e. или а = n / k , или a = 6 n / 2 k + 1. И в том и в другом случае а — рациональное число.

23.8.Период функции cos 3 x / 2равен Т 1= 2π : 3/ 2= 4π/ 3, период функции sin x / 3равен 6π.

Наименьшее общее кратное этих периодов будет 12π. Очевидно, что 12π — период данной функции. Докажем, что это — основной период.

Пусть существует период τ такой, что 0 < τ < 12π. Тогда имеем тождество

cos 3/ 2( x + τ) − sin x + τ/ 3− cos 3/ 2 x + sin x / 3= 0,

или

sin ¾ τ sin ¾ (2 x + τ) + sin τ/ 6cos 1/ 6(2 x + τ) = 0.

Так как τ < 12π, а ¾τ = 3τ/ 4ππ и τ/ 6= τ/ 6ππ, то одно из чисел 3τ/ 4πили τ/ 6π не является целым, т. е. по крайней мере одно из чисел sin ¾τ и sin τ/ 6не равно нулю. Пусть, например, sin ¾τ ≠ 0.

Тогда имеем тождество

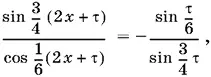
что невозможно, так как в правой части стоит постоянная величина. Легко убедиться, что это тождество ложно, выбрав, например, x = 0 и x = 6π и сравнив для этих x левые части. Получим sin 3τ/ 4= 0, что противоречит предположению.

Ответ.12π.

24.1.Так как sin x − cos² x − 1 = sin² x + sin x − 2 = (sin x + ½)² − 9/ 4, то функция достигает своего наименьшего значения при sin x + ½ = 0.

Ответ. x = (−1) k + 1 π/ 6+ π k .

24.2.Воспользуемся формулой преобразования произведения синусов

y = ½[cos π/ 6− cos (4 x − π/ 6)] = √3/ 4− ½cos (4 x − π/ 6).

Чтобы функция y достигла своего наибольшего значения, нужно положить cos (4 x − π/ 6) = −1, откуда x = π/ 24+ π/ 4(2 n + 1) = π n / 2+ 7π/ 24. Наибольшее значение функции равно y max= √3/ 4+ ½.

Ответ. При x = π n / 2+ 7π/ 24 y max= √3/ 4+ ½.

24.3.Данную функцию можно записать в виде y = sin x cos x (cos² x − sin² x ), после чего она легко преобразуется: 4 y = 2 sin 2 x cos 2 x = sin 4 x .

Ответ.¼.

24.4.Запишем данное выражение в виде ( x + y + 1)² + ( x − 2)² − 3. Оно будет иметь наименьшее значение, если одновременно x − 2 = 0 и x + y + 1 = 0.

Ответ.−3 при x = 2.

24.5.Точки ±1 и ±2 разбивают числовую ось на пять интервалов, в каждом из которых нетрудно найти наименьшее значение y .

1. Если x ≤ −2, то y = x ² − 1 + x ² − 4 − x − 2 − x − 1 = 2 x ² − 2 x − 8.

Абсцисса вершины параболы y = 2 x ² − 2 x − 8 равна x = − b / 2 a = ½,

т. е. при x ≤ 2 мы находимся левее вершины, функция y на этом участке убывает, а потому наименьшее значение она принимает в самой правой точке интервала: x = −2, y = 4.

2. Если [23] Во всех случаях удобно граничную точку относить к обоим интервалам, чтобы не столкнуться с ситуацией, когда наименьшее значение не достигается. −2 ≤ x ≤ −1, то легко проверить, что y = 4.

3. Если −1 ≤ x ≤ 1, то y = −2 x ² + 2 x + 8.

Так как ветви параболы направлены вниз, то наименьшее значение нужно искать на концах интервала: при x = −1 мы уже видели, что y = 4; при x = 1, y = 8.

4. Если 1 ≤ x ≤ 2, то y = 2 x + 6. Наименьшим будет значение в точке x = 1.

5. Если x ≥ 2, то y = 2 x ² + 2 x − 2.

Абсцисса вершины этой параболы x = −½; она лежит левее точки x = 2. Следовательно, наименьшее значение достигается при x = 2, т. е. y = 10.

Ответ. y min= 4 при −2 ≤ x ≤ −1.

24.6.Заменим a / x на сумму из семи одинаковых слагаемых, каждое из которых равно a / 7 x . К функции

x 7+ a / 7 x + a / 7 x + a / 7 x + a / 7 x + a / 7 x + a / 7 x + a / 7 x