Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
1.31.В треугольнике ABC единичной площади проведен отрезок AD , пересекающий медиану CF в точке M , причем FM = ¼ CF . Найдите площадь треугольника ABD .
1.32.Докажите, что произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон (теорема Птолемея) .
1.33.Отрезок, соединяющий середины оснований трапеции, равен их полуразности. Найдите сумму углов при большем основании трапеции.
1.34.Через центр квадрата ABCD проведена прямая, пересекающая сторону AB в точке N , причем AN : NB = 1 : 2. На этой прямой взята произвольная точка M , лежащая внутри квадрата. Докажите, что расстояния от точки M до сторон квадрата AB , AD , BC и CD , взятые в названном порядке, образуют арифметическую прогрессию.
1.35.Квадрат и правильный треугольник, имеющие общую вершину, вписаны в окружность единичного радиуса. Найдите площадь, покрытую и квадратом и треугольником.
1.36.В окружность вписаны равнобедренный остроугольный треугольник площадью S , и трапеция так, что ее большее основание совпадает с диаметром окружности, а боковые стороны параллельны боковым сторонам треугольника. Средняя линия трапеции равна l . Найдите высоту трапеции.
1.37.Найдите отношение площади трапеции ABCD к площади треугольника AOD , где O —точка пересечения диагоналей трапеции, если известно, что 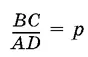 .
.
1.38.Два правильных многоугольника с периметрами a и b описаны около окружности, а третий правильный многоугольник вписан в эту окружность. Второй и третий многоугольники имеют каждый вдвое больше сторон, чем первый. Найдите периметр третьего многоугольника.
1.39.Внутри угла AOB , меньшего π, дана точка M , находящаяся на расстоянии а от вершины угла. Отрезок ОМ образует углы α и β со сторонами угла AOB . Найдите радиус R окружности, проходящей через M и отсекающей на сторонах угла AOB хорды, равные 2 а .
1.40.Из внешней точки A проведены две взаимно перпендикулярные секущие ABD и ACE к окружности с центром O . Площади треугольников ABC и АDЕ относятся как m : n . Определите величины дуг BC и DЕ , каждая из которых меньше полуокружности.
1.41.Из точки А , лежащей на окружности радиуса r , проведены две хорды AC и AB . Эти хорды лежат по одну сторону от диаметра окружности, проходящего через точку А . Длина большей хорды равна b , а угол ВАС равен α. Найдите радиус окружности, которая касается хорд AB и AC и дуги BC .
1.42.Даны две концентрические окружности радиусов R и r ( R > r ). Найдите сторону квадрата, две вершины которого лежат на одной окружности, а две другие — на другой. При каком соотношении между радиусами данных окружностей решение задачи возможно и при каком соотношении задача имеет единственное решение?
1.43.В сегмент, дуга которого содержит 120°, вписан квадрат. Определите сторону квадрата, если радиус R круга равен 2 + √19 .
1.44.У равнобочной трапеции с б о ́льшим основанием а и острым углом α высота вдвое меньше меньшего основания. На меньшем основании, как на диаметре, построена окружность. Найдите радиус окружности, касающейся построенной окружности, большего основания и боковой стороны.
1.45. AB и CD — два взаимно перпендикулярных диаметра окружности S 1. С центром в точке D радиусом BD построена окружность S 2. Из точки D проведены две прямые, пересекающие окружность S 1в точках P и Q и дугу AB окружности S 2, заключенную внутри окружности S 1, в точках M и N . Точки P и Q спроецированы на AB ; P 1и Q 1соответственно — их проекции. Докажите, что фигура RMNQ равновелика треугольнику P 1 Q 1 D .
1.46.Через точку P , лежащую вне окружности с центром O и радиусом R , проходят две взаимно перпендикулярные секущие. Первая секущая пересекает окружность в точках А и С (точка С лежит между P и А ), а вторая секущая — в точках В и D ( D лежит между P и В ). Пусть Р 1— проекция P на AB , а M — одна из точек пересечения AB с окружностью, центр которой Р 1, а радиус Р 1 О . Найдите длину МР .
1.47.Найдите угол между двумя хордами, пересекающимися внутри окружности, если точка их пересечения удалена от центра окружности на 3 / 5ее радиуса и делит одну хорду пополам, а другую — в отношении 4 : 9.
1.48.Дан сектор ОАВ ( O — центр) с центральным углом в 90° и радиусом R . На отрезке ОВ , как на диаметре, построена полуокружность, лежащая внутри сектора. Найдите радиус окружности, касающейся этой полуокружности и отрезков ОА и AB .
1.49.В круге проведена хорда AB , пересекающая диаметр DE круга в точке M и наклоненная к нему под углом φ. Дано, что 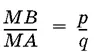 , где p и q — известные числа. Из точки В проведена хорда BC , перпендикулярная к диаметру DE , и точка С соединена с точкой А . Найдите площадь треугольника ABC , если радиус круга равен R .
, где p и q — известные числа. Из точки В проведена хорда BC , перпендикулярная к диаметру DE , и точка С соединена с точкой А . Найдите площадь треугольника ABC , если радиус круга равен R .
1.50.Площадь треугольника равна S , а длины его сторон образуют арифметическую прогрессию, разность которой равна d . Найдите радиус описанной окружности.
1.51.В треугольнике ABC точка P лежит на стороне AB и AB = 2 АР , точка Q — на стороне BC и BC = 4 BQ , точка R — на стороне AC и AC = 5 АВ . Отрезки PQ и BR пересекаются в точке T . В каком отношении точка T делит отрезок PQ ?
1.52.В треугольнике PQR на стороне PQ взята точка N а на стороне РR — точка L . Отрезки QL и RN пересекаются в точке T . Дано QN = RL , QT : TL = m : n . Найдите PN : PR .
1.53.Две окружности с центрами О 1и О 2пересекаются в точках M и N . Точка О 2лежит на первой окружности. Найдите периметр фигуры, являющейся пересечением данных окружностей, если 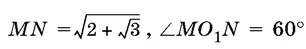 .
.
Интервал:
Закладка:










