Генри Дьюдени - Кентерберийские головоломки

– По той же причине, – заметил он, – если бы биллиардный стол представлял собой правильную плоскость, то все шары должны были бы собраться в центре.

Хотя Джордж и попытался пояснить свою мысль, положив визитную карточку на апельсин и растолковывая закон всемирного тяготения, миссис Олгуд отказалась признать этот факт. Она не могла понять, что крышка настоящего биллиардного стола теоретически должна иметь сферическую форму, подобно кусочку кожуры апельсина, который чистил Джордж. Разумеется, стол настолько мал по сравнению с поверхностью Земли, что кривизну невозможно обнаружить, но тем не менее теоретически она присутствует. Поверхность, которую мы называем плоской, не идентична идеальной математической плоскости.

– Дядя Джон, – снова вмешался в разговор Билли Олгуд, – между Англией и Францией есть один остров, и все же этот остров расположен от Франции дальше, чем Англия. Что это за остров?

– Это выглядит абсурдным, мой мальчик; ибо если я приму этот бокал за остров и поставлю его между, двумя тарелками, то кажется совершенно невозможным, чтобы бокал отстоял от любой из тарелок дальше, чем они друг от друга.

– А разве Гернси не расположен между Англией и Францией? – спросил Билли.

– Да, конечно.

– Ну так вот, я думаю, дядя, вы сумеете определить, что Гернси расположен примерно в двадцати шести милях от Франции, а расстояние между Францией и Англией в районе Дувра и Кале равно только двадцати одной миле.

– Мой учитель математики, – сказал Джордж, – пытался внедрить в мое сознание аксиому, что если равные величины умножить на равные, то снова получатся равные величины.

– Это само собой очевидно, – вставил мистер Филкинс. – Например, если 3 фута равны 1 ярду, то дважды по 3 фута равно 2 ярдам. Не правда ли?

– Но мистер Филкинс, – спросил Джордж, – не равен ли этот бокал, наполовину наполненный водой, такому же сосуду наполовину пустому?

– Конечно, Джордж.

– Тогда из этой аксиомы следует, что полный бокал равен пустому. Правильно ли это?

– Нет, разумеется, нет. Я никогда не задумывался над этим в таком плане.

– Может быть, – предположил мистер Олгуд, – эта правило не применимо к жидкостям.

– Но было бы совсем нелепо, – сказал с улыбкой Джордж, – если бы мы должны были исключить и твердые тела. Например, возьмем участок земли. Одна миля в квадрате равна одной квадратной миле. Следовательно, две мили в квадрате должны равняться двум квадратным милям. Не так ли?

– Постойте-ка. Ну конечно, нет, – сказал мистер Филкинс, – поскольку две мили в квадрате равны четырем квадратным милям.

– Тогда, – сказал Джордж, – если аксиома не справедлива в этих случаях, когда же она справедлива?

Мистер Филкинс обещал подумать над этим вопросом, и, может быть, читатель тоже поразмыслит об этом на досуге.

– Послушайте-ка, Джордж, – сказал его кузен Реджинальд Були, – на сколько четыре четвертых превосходят три четвертых?

– На одну четвертую! – воскликнули все одновременно.

– Спроси еще что-нибудь, – предложил Джордж.

Некоторые из присутствующих не смогли понять, что правильным ответом будет «одна треть», хотя Реджинальд пытался объяснить, что если три каких-нибудь предмета увеличить на одну треть, то получится четыре предмета.

– Может ли кто-нибудь из вас быстро записать с помощью цифр «двенадцать тысяч двенадцать сотен двенадцать»? – спросил мистер Олгуд.

У его старшей дочери, миссис Милдред, у единственной оказался под рукой карандаш.

– Это невозможно сделать, – заявила она после нескольких попыток на белоснежной скатерти; но мистер Олгуд показал ей, что можно записать « ₤ 13 212».

– Теперь моя очередь, – сказала Милдред. – Я хочу всем задать вопрос. При царе Ироде во время избиения младенцев много бедных Малюток закопали в песок, так что лишь их ножки торчали наружу. Как смогли бы вы отличить мальчиков от девочек?

– Я думаю, – сказала миссис Олгуд, – что здесь какой-то подвох, что-нибудь связанное с их бедными маленькими душами.

После того как все сдались, Милдред напомнила всей компании, что избиению подвергались лишь мальчики.

– Когда-то давным-давно, – начал Джордж, – Ахиллес состязался в беге с черепахой…

– Стоп, Джордж! – вмешался мистер Олгуд. – Мы не станем здесь касаться этого вопроса. Я знал в молодости двух человек, которые были закадычными друзьями, но поссорились из-за этой дьявольской выдумки Зенона так, что уже не разговаривали друг с другом до конца своей жизни. Я подвожу черту под ней да еще под одной глупой шуткой Зенона, касающейся летящей стрелы. Я не думаю, чтобы кто-нибудь их понимал, поскольку сам я никогда их не мог понять.

– Очень хорошо, отец. Вот кое-что другое. Почтовое ведомство решило провести линию телеграфных столбов через высокий холм между Тёрмитвилем и Вёрцльтоном, но оказалось, что железнодорожная компания прокладывает путь в том же направлении, делая глубокую выемку грунта. Поэтому решили ставить столбы вдоль этого пути, который шел на постоянном уровне. Далее, столбы должны располагаться на расстоянии ста ярдов друг от друга, длина линии через холм равна пяти милям, а длина соответствующего участка железнодорожного пути составляет лишь четыре с половиной мили. Сколько столбов сэкономили, решив проводить линию вдоль железнодорожного пути!

– Это очень просто подсчитать, – сказал мистер Филкинс. – Определим, сколько раз сто ярдов укладывается в пяти милях и сколько в четырех с половиной. Затем вычтем из одного другое и получим число сэкономленных столбов.

– Совершенно верно, – подтвердил мистер Олгуд. – Нет ничего проще.

– Именно это сказали и работники почтового ведомства, – заметил Джордж, – но это совершенно не верно. Если вы посмотрите вот на этот рисунок, который я здесь набросал, то заметите, что нет вовсе никакой разницы. Если столбы должны располагаться на расстоянии в сто ярдов, то их потребуется при проводке линии вдоль поверхности холма ровно столько же, сколько и при проводке ее вдоль железнодорожного пути.

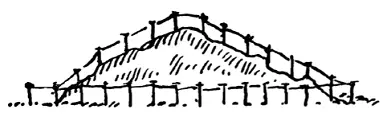
– Ты, конечно, ошибаешься, Джордж, – сказала миссис Олгуд, – ведь если столбы располагаются друг от друга на расстоянии в сто ярдов, а путь увеличивается на полмили, то на эти полмили потребуются дополнительные столбы.

– Посмотри-ка на рисунок, мама. Ты можешь заметить, что расстояние между столбами не совпадает с расстоянием между их основаниями, измеренными вдоль поверхности земли. Когда я стою на ковре, то нахожусь от тебя ровно на таком же расстоянии, как если бы я, не сходя с этого места, залез сейчас на стул.