Генри Дьюдени - Кентерберийские головоломки

15. Было 4 порции пирога и 4 порции печеночного паштета, которые следовало распределить среди 8 из 11 паломников. Но 5 из этих 11 хотят есть только пирог, 4 – только паштет, а 2 – и то и другое блюдо. Любая возможная комбинация должна попасть в одну из следующих групп: 1) пирог распределяется целиком между первыми пятью из упомянутых паломников; 2) только одному из «всеядной» пары дается пирог; 3) пирог дается другому из этой пары; 4) пирог дается обоим из этой пары. Число возможных комбинаций соответственно равно: 1) 75; 2) 50; 3) 10; 4) 10, что в общей сложности дает 145 способов выбора восьми участников. В большинстве случаев называют ответ 185, просмотрев то обстоятельство, что в сорока случаях в группе (3) еду получают те же самые 8 гостей, что и в группе (2), хотя «всеядная» пара и ест предложенные блюда по-разному. Именно в этом месте просчиталась вся компания.

16. Числом, которое Пристав церковного суда назвал по секрету Батской ткачихе, было 29, а начать счет ей следовало с Доктора медицины, который стоял непосредственно справа от нее. Первый раз 29 выпадает на Шкипера, который выходит из круга. Второй раз счет падает на Доктора, который выбывает следующим. Оставшиеся три раза счет выпадает соответственно на Повара, Пристава и Мельника. Следовательно, все леди остались бы на ночлег в таверне, если бы не роковая сшибка доброй ткачихи. Вместо 29 можно было бы взять любое кратное 2520 плюс 29, причем счет следовало начинать с Доктора.

17. Монах мог поместить собак в конуры 2926 различными способами так, чтобы на каждой стороне было по 10 собак. Число собак может изменяться от 20 до 40; в этих пределах всегда можно расположить собак нужным способом.

Решение этой головоломки в общем виде не просто. В случае п собак на каждой стороне квадрата число различных способов равно

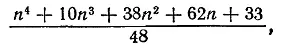
при п нечетном и

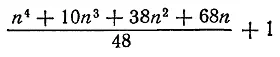
при п четном, если считать только те размещения, которые существенно различны. Но если мы будем считать все перевернутые и отраженные размещения различными, как и поступал сам Монах, то п (четное или нечетное) собак можно разместить

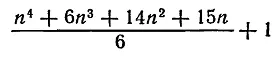
способами. Дабы возможно было поместить по п собак на каждой стороне, их число должно быть не меньше 2п и не больше 4п , но внутри этих границ его молено взять любым.

Обобщение принципа, лежащего в основе этой головоломки, приведено в задаче 42.

18. Существует 264 различных способа, которыми шхуна «Маделена» могла совершить десять ежегодных плаваний, не проходя ни по какому пути дважды. Каждый год она должна заканчивать плавание на том же острове, откуда она впервые отчалила.

19. Аббат из Черси был совершенно прав. Этот крест странной формы можно разрезать на четыре части, из которых затем удается сложить правильный квадрат. Как это сделать, показано на рисунке.

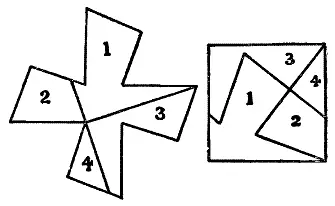
20. Здесь мы действительно сталкиваемся с запутанной задачей. Наши учебники сообщают, что все сферы подобны и что соответствующие объемы относятся, как кубы линейных размеров. Следовательно, поскольку окружности [31]двух сосудов равны соответственно одному и двум футам, а кубы единицы и двух в сумме дают 9, то нам остается только найти два других числа, сумма кубов которых равнялась бы 9. Разумеется, эти числа должны быть дробными. Кстати, этот маленький вопрос привлекал внимание образованнейших людей своего времени на протяжении двух с половиной столетий. Хотя Ферма в XVII в. показал, как можно найти ответ из двух дробей со знаменателем, содержащим не менее чем 21 цифру, этим исчерпываются не только все опубликованные ответы, полученные с помощью его метода, который я нашел неточным, но и никогда не публиковавшийся много меньший результат, приведенный ниже. Кубы чисел

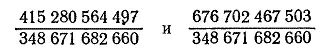
6 сумме дают ровно 9, и, следовательно, такими долями фута должны выражаться длины окружностей двух сосудов, про которые Доктор сказал, что они должны вместе содержать такое же количество жидкости, как и показанные два сосуда. Один выдающийся клерк страховой компании и еще один корреспондент взяли на себя труд возвести в куб эти числа, и они оба нашли мои ответ совершенно правильным.

Если бы исходные сосуды имели в окружности соответственно 1 и 3 фута, то ответом служили бы числа

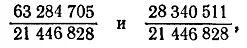
сумма кубов которых равна 28. (См. также головоломку 61.)

Зная какое-то выражение числа в виде суммы или разности двух кубов, мы можем по формуле получить отсюда бесконечно много других представлений этого числа с помощью попеременно положительных и отрицательных чисел. Так, Ферма, отправляясь от известного равенства 1 3+ 2 3= 9 (которое мы назовем основным), сначала получил решение из больших отрицательных чисел, а затем решение из еще больших положительных чисел. Но существует бесконечно много основных соотношений, и я с помощью ряда проб нашел исходное решение из отрицательных чисел (меньших, чем те, что на первом шаге получил Ферма), из которого я уже и вывел решение, указанное выше. Это простое объяснение.

О любом числе до 100, за исключением 66, мы можем сказать, представимо ли оно в виде суммы двух кубов или нет. Студентам следует обратиться к курсу теории чисел.

Несколько лет назад я опубликовал решение для случая

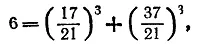
для которого Лежандр привел обстоятельное «доказательство» невозможности такого представления, но я обнаружил, что Люка предвосхитил появление моего решения.

21. На рисунке показано, как можно посадить 16 деревьев, чтобы они образовали 15 рядов по 4 дерева в каждом ряду. Это число рядов больше того, которое уже давно считалось максимальным. Хотя при нынешнем уровне наших знаний невозможно строго доказать, что число 15 нельзя превзойти, тем не менее я свято верю в то, что это максимально возможное число рядов.