Генри Дьюдени - Кентерберийские головоломки

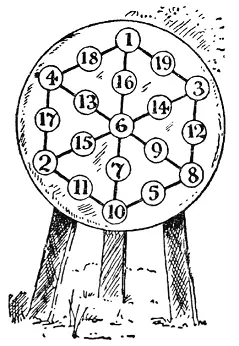
Мне кажется, что относительно решения де Фортибуса стоит добавить несколько замечаний. Девятнадцать чисел можно расположить таким образом, чтобы сумма вдоль каждой прямой равнялась любому числу от 22 до 38 включительно, кроме 30, В некоторых случаях существует несколько различных решений, но в случае 23 их только два. Я привел одно из них. Чтобы получить другое, поменяйте на рисунке местами 7, 10, 5, 8, 9 соответственно с 13, 4, 17, 2, 15. Также поменяйте местами 18 с 12, а остальные числа оставьте на прежних местах. В каждом случае в центре должно находиться четное число; им может оказаться любое число от 2 до 18. У каждого решения есть дополнительное к нему решение. Таким образом, если вместо каждого числа на приведенном рисунке мы поставим разность между ним и 20, то получим решение для случая 37. Аналогичным образом из расположения на исходном рисунке мы сразу же получим решение для случая 38.

36. Сэр Хьюг весьма озадачил своего главного зодчего, потребовав от него построить окно, у которого каждая сторона равнялась бы одному футу и которое было бы разделено железными прутьями на восемь одинаковых просветов с равными сторонами. На рисунке показано, как это можно сделать.

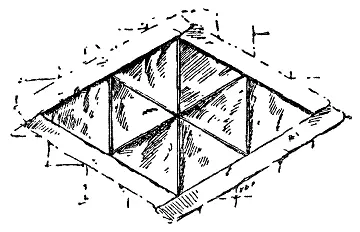
Нетрудно заметить, что стороны окна равны одному футу, а каждая сторона треугольных просветов составляет половину фута.

– По правде говоря, мой добрый зодчий, – сказал лукаво де Фортибус, обращаясь к мастеру, – я не требовал от тебя, чтобы окно было квадратным; совершенно ясно, что оно и не может быть таковым.

37.

– Клянусь пальцами святого Модена, – воскликнул сэр Хьюг де Фортибус, – мой бедный ум никогда не придумывал ничего более искусного и более занимательного. Меня словно озарило, и теперь, по прошествии некоторого времени, я все больше восхищаюсь головоломкой, которая представляется мне все труднее и труднее. Мои господа и родичи, я сейчас покажу вам, как она решается.

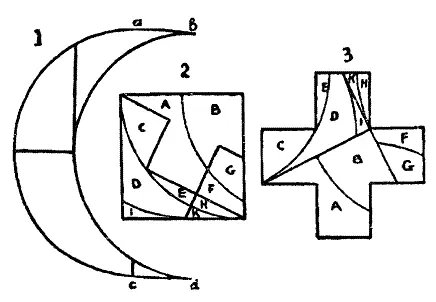
Затем достойный рыцарь указал на слегка неправильную форму полумесяца – его два участка от а до d и от с до d представляют собой отрезки прямых, а дуги ас и bd в точности одинаковы. Если сделать разрезы, показанные на рисунке 1 , то из четырех получившихся частей ( кривые на рисунке 2) можно сложить правильный квадрат. Если теперь этот квадрат разрезать ( прямые на рисунке 2), то мы получим 10 частей, из которых можно будет затем сложить симметричный греческий крест, который вы видите на рисунке 3. Пропорции полумесяца и креста на исходном рисунке были указаны правильно, и можно показать, что решение получается абсолютно точное, а не приближенное.

Мне известно решение с существенно меньшим числом частей, но его значительно труднее понять, чем приведенное, где все упрощается введением промежуточного квадрата.

38. Головоломка состояла в том, чтобы, начиная от верхнего А и двигаясь вниз от одной соседней буквы к другой, подсчитать, сколькими различными способами можно прочитать слово ABRACADABRA.

– Теперь обратите внимание, добрые друзья мои, – сказал сэр Хьюг, обращаясь ко всем, кто находился рядом, – что вначале есть два пути: вы можете выбрать любое В, затем любое R и так далее до самого конца. До каждой из букв можно добраться, двигаясь от верхнего А, соответственно 2, 4, 8, 16, 32 и т. д. способами. Следовательно, поскольку нужно сделать 10 шагов, спускаясь от верхнего А до нижней строки, нам остается только умножить 2 на себя 10 раз. В результате мы и получим искомое число, равное 1024.

39. Хотя сэр Хьюг и заявил, что нет нужды измерять шест, все же совершенно необходимо было определить его высоту. Друзьям и домочадцам сэра Хьюга де Фортибуса было хорошо известно, что он имел шесть футов росту. На исходном рисунке можно заметить, что рост сэра Хьюга в два раза больше длины его тени. Следовательно, высота флагштока в том же месте и в то же время дня тоже должна вдвое превышать длину его тени. Длина тени флагштока равна росту сэра Хьюга, следовательно, она составляет 6 футов, а высота флагштока – 12 футов. Далее, улитка, поднимаясь на 3 фута днем и опускаясь на 2 фута ночью, поднимается в действительности за сутки на 1 фут. В конце девятых суток она окажется в трех футах от вершины и, значит, закончит свое путешествие на десятый день.

Читатель, безусловно, воскликнет здесь:

– Все это очень хорошо, но как мы могли узнать рост сэра Хьюга? О нем ничего не говорилось!

Действительно, прямо на это не указывалось, но для людей искушенных не составит труда его определить. На рисунке к задаче 36 сэр Хьюг изображен у квадратного окна, про которое сказано, что его сторона равна 1 футу. Следовательно, отложив эту длину (нужное число раз), можно было убедиться, что рост сэра Хьюга в 6 раз превышает высоту окна, то есть равен 6 футам!

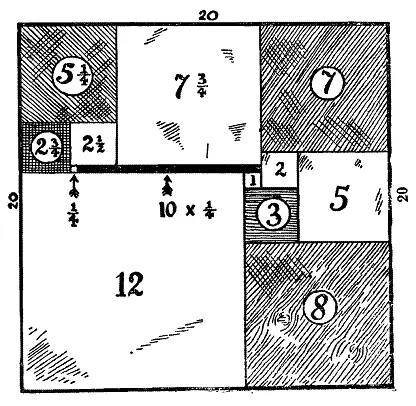
40. Последняя головоломка была, без сомнения, крепким орешком, но, надо думать, трудности не делают хорошую головоломку менее интересной, когда нам покажут ее решение. На приведенном здесь рисунке показано, как была выложена крышка у шкатулки леди Изабеллы де Фитцарнульф. Это единственное возможное решение, и удивительно (хотя я и не могу привести здесь довольно тонкий метод решения), что число, размеры и порядок расположения квадратов определяются размерами золотой полоски и что крышка шкатулки не может иметь других размеров, отличных от 20 квадратных дюймов. Число, указанное в каждом квадрате, равно длине его стороны, выраженной в дюймах, так что ответ можно проверить почти с одного взгляда.

Сэр Хьюг сделал несколько общих замечаний, которые не совсем безынтересны и сегодня.

– Друзья и домочадцы, – сказал он, – если те странные порождения моего бедного ума, о которых мы так приятно поговорили сегодня вечером, и оказались, быть может, малоинтересными для вас, пусть они послужат напоминанием разуму о том, что наша быстротекущая жизнь окружена и наполнена загадками.

41. Перенумеруйте корзинки, показанные на исходном рисунке, от 1 до 12 в направлении, в котором, как мы видим, двигается брат Джонатан. Начиная от 1, действуйте, как указано ниже, причем «1 в 4» означает, что надо взять рыбку из корзинки 1 и переложить ее в корзинку 4.