Генри Дьюдени - 200 знаменитых головоломок мира

На доске с n 2клетками два ферзя, две ладьи, два слона или два коня всегда можно расположить (безотносительно к тому, атакуют ли они друг друга или нет) 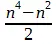способами. Следующие формулы показывают, сколькими из способов две фигуры можно расположить при условии взаимной атаки и без нее.

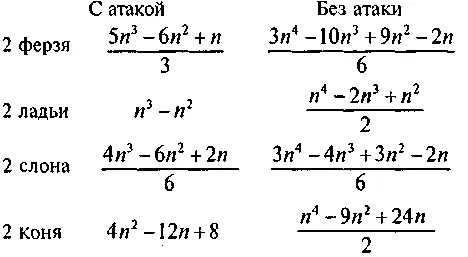
(См. головоломку «Охота на льва».)

147. Турне ладьи.Единственную ладью требуется передвигать по всей доске так, чтобы она посетила каждую клетку ровно по одному разу и закончила свое турне в той клетке, с которой его начала. При этом следует сделать как можно меньшее число ходов, но если вы будете не очень внимательны, то совершите ровно на один ход больше, чем нужно. Разумеется, клетка считается «посещенной» как в случае, если вы просто проходите через нее, так и в случае остановки в ней. Нас не должны волновать софизмы вроде того, что мы дважды посещаем исходный квадрат. Будем считать, что мы посещаем его один раз.

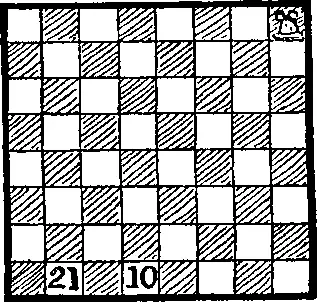
148. Путешествие ладьи.В названии этой головоломки я не случайно употребил слово «путешествие», поскольку слово «турне» означает возвращение в исходное место, а в данном случае мы не будем этого делать. Ладья делает 21 ход, посетив каждую клетку доски ровно по одному разу, останавливается в клетке 10 в конце десятого хода и заканчивает путешествие в клетке 21. Два последовательных хода нельзя делать в одном и том же направлении; другими словами, вы должны поворачивать после каждого хода.

149. Еще одна томящаяся дева.Злой барон в добрые старые времена заточил одну невинную деву в глубокую темницу, которая находилась подо рвом замка. На рисунке вы видите 63 камеры темницы, которые соединены между собой открытыми дверьми, и камеру, где прикована дева. Некий доблестный рыцарь, который любил эту деву, сумел вызволить ее из рук врага. Добравшись до входа в темницу, как показано на рисунке, он затем дошел и до камеры, где томилась дева, посетив по дороге каждую камеру ровно по одному разу. Возьмите карандаш и попытайтесь обозначить его путь. Преуспев в этом, попробуйте свести этот путь к 22 прямолинейным отрезкам. Это можно сделать, по-прежнему не посетив ни одну камеру дважды.

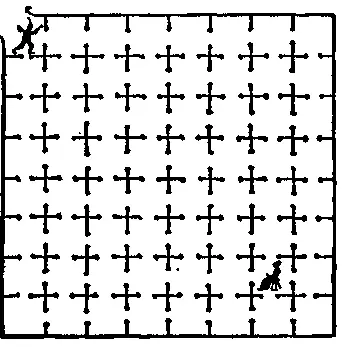
150. Подземелье.Случилось когда-то во Франции, что один узник за собственные ли грехи или грехи чужие был брошен в подземелье, где насчитывалось 64 камеры, связанные между собой открытыми дверьми, как показано на рисунке. Дабы чем-то скрасить однообразие заточения, он придумывал себе разные головоломки. Вот одна из них.

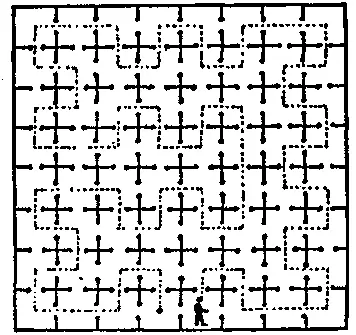
Как, начиная с указанной на рисунке камеры, он мог бы посетить каждую камеру ровно по одному разу, сделав при этом как можно больше поворотов? Первая попытка узника отмечена на рисунке пунктиром. Можно заметить, что путь узника состоит из 55 прямолинейных участков, но после многих попыток ему удалось улучшить этот результат. Можете ли вы получить, большее число отрезков? Заканчивать путь разрешается в любой камере. Попробуйте решить головоломку с карандашом в руках на шахматной доске. При желании вы можете рассматривать прямолинейные участки как ходы ладьи.

151. Лев и человек.Некогда на одной из людных площадей Рима находилась тюрьма. Она представляла собой 64 камеры под открытым небом, которые соединялись между собой, как показано на рисунке. За происходившими в ее стенах состязаниями наблюдали с высокой башни. Толпу особенно увлекало зрелище того, как в лабиринте камер искали друг друга (или избегали) христианин и лев. Их помещали в диаметрально противоположные камеры при всех открытых дверях. Как-то человеку дали в руки меч. Он оказался не из трусливых и старался найти льва так же, как лев, несомненно, искал его.

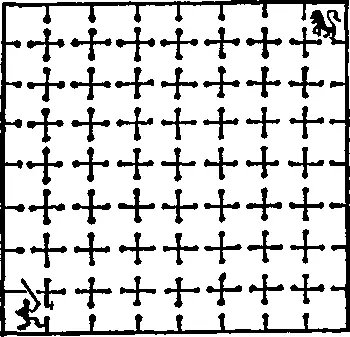
Человек посетил каждую камеру ровно по одному разу, преодолев наименьшее возможное число прямолинейных участков пути, пока не достиг камеры, где первоначально находился лев. Лев, как это ни странно, тоже посетил каждую камеру ровно по одному разу, пробежав наименьшее возможное число прямолинейных участков пути, пока не добрался до камеры, где первоначально находился человек. Они покинули исходные камеры одновременно, двигались с одинаковой скоростью, и хотя порой мелькали в поле зрения друг друга, но так ни разу и не встретились. Головоломка состоит в том, чтобы показать путь каждого из них.

152. Визиты слона.Белые клетки на шахматной доске изображают те места, которые хочет посетить слон. Поместите слона на любую, какую пожелаете, клетку, и сделайте так, чтобы он мог посетить все желаемые места (делая обычные ходы слона) за наименьшее число ходов. Разумеется, все клетки, через которые он проходит, считаются «посещенными». Вы можете посетить любую клетку более одного раза, но вам не разрешается передвигаться дважды между одними и теми же смежными клетками. Чему равно наименьшее число ходов? Слон не обязан заканчивать свои визиты в том же месте, откуда отправился.

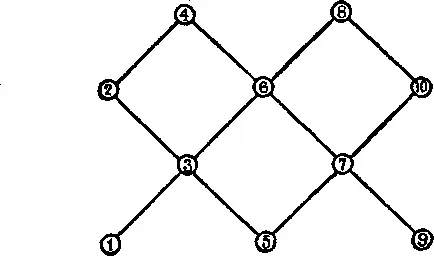
153. Новая головоломка с шашками.Вот одна новая головоломка с передвигающимися шашками или монетами, которая на первый взгляд должна выглядеть невероятно простой, но затем окажется, что над ней нужно поломать голову. Я привожу ее здесь по причинам, которые выяснятся, когда мы перейдем к следующей головоломке. Перерисуйте на листе бумаги в увеличенном виде приведенную здесь схему; затем поставьте 2 белые шашки на кружки 1 и 2, а две красные шашки — на кружки 9 и 10. Головоломка состоит в том, чтобы поменять белые и красные шашки местами. За один раз вы можете передвинуть любую шашку вдоль любой прямой, соединяющей кружки, с тем единственным ограничением, что красная шашка никогда не должна находиться на одной прямой с белой шашкой. Так, первый ход можно делать лишь с 1-й или 2-й на 3-ю либо с 9-й или 10-й на 7-ю.

154. Новая головоломка со слонами.Это весьма занимательная маленькая головоломка. Поставьте 8 слонов (4 черных и 4 белых) на уменьшенную шахматную доску, как показано на рисунке. Задача состоит в том, что бы поменять черных и белых слонов местами, причем ни один слон не должен ни разу атаковать слона противоположного цвета. Они должны ходить по очереди — сначала белый, затем черный, потом снова белый и т. д. Когда вам удастся это сделать, попытайтесь найти наименьшее число ходов.