Генри Дьюдени - 200 знаменитых головоломок мира

В первом случае числа образуют арифметическую прогрессию: 1, 1½, 2½ , 3, 3½, 4, 4½, 5.

Но из любых девяти чисел можно образовать магический квадрат, если их удается расположить следующим образом:

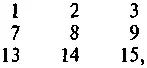
где разности по горизонталям все одинаковы так же, как и разности по вертикалям, хотя последние и не обязаны совпадать с первыми. Именно так обстоит дело в случае второго решения, где числа можно записать в виде:

Точно так же в решении задачи 67 с монетами числа в шиллингах равны

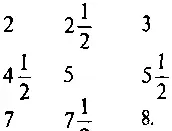
Если должно быть девять различных чисел, то 0 может появиться один раз (как в решении задачи 22). И все же можно построить квадрат с отрицательными числами следующим образом:

69.Как совершенно верно заметил Профессор, существует только одно решение (если не считать симметричного) этой головоломки. На другие бокалы прыгают следующие лягушки: Джордж в третьем (сверху) горизонтальном ряду; Чанг — искусно выполненное существо в конце четвертого ряда и Вильгельмина — прекрасное создание в седьмом ряду. Джордж прыгает вниз на второй бокал седьмого ряда; Чанг, который из-за хронического ревматизма может совершать лишь небольшие прыжки, перемещается довольно неохотно на бокал, расположенный непосредственно над ним (восьмой в третьем ряду), тогда как Вильгельмина со всем пылом юности и пола совершает отличный и сложный прыжок на четвертый бокал четвертого ряда. При новом расположении, как видно из рисунка, никакие две лягушки не находятся на одной вертикали, горизонтали или диагонали.

70.Эта головоломка довольно трудна, хотя, как заметил Профессор, когда Хокхерст нашел решение, «она как раз из тех, которые решаются... с первого взгляда», если повезет. И все же если посмотреть на изящное симметричное решение, то оно выглядит невероятно простым.

Можно заметить, что Ромео добирается до балкона Джульетты, посетив каждый дом только по одному разу и сделав при этом 14 поворотов, если не считать поворота, который он делает в самом начале. Это наименьшее возможное число поворотов, и задачу можно решить, лишь выбрав путь, указанный на рисунке или симметричный ему.

71.Для того чтобы совершить свое путешествие с наименьшим числом поворотов, Ромео должен избрать указанный мною путь, при котором приходится сделать лишь 16 поворотов. Профессор сообщил мне, что Helix aspersa, то есть обыкновенная, или садовая, улитка, испытывает странную неприязнь к поворотам, она настолько велика, что один представитель этого вида, с которым он проводил эксперименты, отправился однажды вечером по прямой и с тех пор так и не повернул назад.

72.Это одна из тех головоломок, где практически невозможно избежать неоднозначности решения. Имеются два или три положения, на которые четыре лягушки могут прыгнуть таким образом, чтобы образовалось пять прямых, по четыре лягушки на каждой, но решение, приведенное на рисунке, наиболее удовлетворительно.

Прыгавшие лягушки оставили свои призраки на прежних местах, дабы показать читателю, где они находились ранее. Чанг, лягушка в середине верхнего ряда, страдающая ревматизмом, о чем уже говорилось в задаче о лягушках и бокалах, делает самый короткий прыжок — на небольшое расстояние между двумя рядами; Джордж и Вильгельмина прыгают с концов нижнего ряда в направлении север-северо-запад и север-северо-восток соответственно, тогда как лягушка из середины нижнего ряда, чье имя Профессор забыл упомянуть, прыгает точно на юг.

73.Дабы выиграть в эту игру, вы должны рано или поздно оставить сопернику четное число одинаковых групп. Затем, что бы он ни делал в одной группе, вы повторяете то же самое в такой же группе. Пусть, например, вы оставили ему следующие группы: 0.0.000.000. Теперь если он собьет одну кеглю, то и вы сбиваете одну кеглю; если он собьет две из одного триплета, то и вы сбиваете две из другого триплета; если он собьет центральную кеглю в одном из триплетов, то и вы сбиваете центральную кеглю другого триплета. Таким путем вы должны выиграть при известных обстоятельствах. Поскольку игра начинается с расположения 0.00000000000, первый игрок может всегда выиграть, но только при условии, что он собьет шестую или десятую кеглю (считая одну, уже упавшую, второй), и это в любом случае приведет к расположению 0.000.0000000, поскольку порядок групп роли не играет. Что бы теперь ни сделал второй игрок, всегда можно добиться четного числа равных групп. Предположим, что он сбивает одинокую кеглю, тогда мы оставляем ему расположение 00.0000000. Далее, что бы он ни делал, мы затем оставляем ему либо 000.000, либо 0.00.000. Мы уже знаем, что в первом случае выигрыш обеспечен, но он обеспечен и во втором случае, ибо, как бы противник ни играл, мы всегда можем поставить его либо перед 0.0, либо перед 0.0.0.0, либо перед 00.00. Провести полный анализ я предоставляю читателю.

74.На рисунке показано, как из 13 частей можно сложить шахматную доску (следует заметить, что обратная задача о вырезании из доски этих специальных частей занимательна в равной степени).

75.Представьте себе, что комната — это картонная коробка. Тогда ее можно разрезать многими способами и развернуть на стол. Я показываю четыре таких способа и отмечаю в каждом случае относительное расположение паука и мухи и прямой путь, которым, не сходя с картона, должен двигаться паук. Это четыре наиболее благоприятных случая, и можно заметить, что кратчайшим будет путь 4, поскольку он равен всего лишь 40 футам (сложите 32 в квадрате с 24 в квадрате и извлеките квадратный корень). Легко видеть, что на самом деле паук ползет по пяти из шести различных сторон комнаты! Отметив путь, сложите вновь коробку (удалив сторону, по которой паук не ползет), и вид наикратчайшего пути окажется довольно удивительным. Если бы паук придерживался пути, который большинству, очевидно, покажется кратчайшим (путь 7), то ему пришлось бы проделать 42 фута! На пути 2 расстояние составило бы 43,174 фута, а длина пути 3 оказалась бы равной 40,718 фута. Я предоставляю читателю определить наикратчайшие пути, когда паук и муха находятся соответственно от потолка и пола на расстояниях 2, 3, 4 и 5 футов.