Генри Дьюдени - 200 знаменитых головоломок мира

Если мы сложим цифры любого числа и затем, если потребуется, повторим эту процедуру, то в конце концов мы получим однозначное число. Я называю его «цифровым корнем». Так, цифровой корень 521 равен 8, а 697 — 4. Далее: очевидно, что цифровые корни двух искомых чисел должны давать одинаковый корень в сумме и произведении. Это может быть лишь в случае, когда корни двух чисел равны 2 и 2, или 9 и 9, или 3 и 6, или 5 и 8. Следовательно, цифровой корень двузначного сомножителя должен равняться 2, 3, 5, 6, 8 или 9. В каждом случае есть 10 таких чисел. Я выписал все 60, затем я вычеркнул те из них, у которых вторая цифра превосходит первую и у которых обе цифры совпадают (всего 36 чисел); затем я вычеркнул те числа, где первая цифра нечетна, а вторая четна (7 чисел); затем — все кратные 5 (еще 3 числа). Числа 21 и 62 я отверг после исследования, в детали которого не хочу здесь входить. Теперь из первоначальных 60 чисел осталось только 12 следующих: 83, 63, 81, 84, 93, 42, 51, 87, 41, 86, 53 и 71. Это единственные возможные множители, которые мне пришлось изучить.

Теперь мои действия стали столь же удивительными, как и простыми. Сначала, изучая 83, я вычитаю 10 и получаю 73. Добавляя нули ко второй цифре, я говорю, что если 30 000 и т. д., разделенное на 73, даст когда-либо в остатке 43, то частное и будет искомым множителем для 83. Этим путем я получил 43. Единственным кратным 3, дающим 8 на месте единиц, является 6. Следовательно, я умножаю 73 на 6 и получаю 438, или 43 после отбрасывания 8. Далее: при делении 300000 на 73 получается остаток 43, а частное равно 4109. К этому я добавляю уже упомянутое 6 и получаю пример чародея 41 096 × 83.

Исследуя четные числа, разберем два случая. Так, взяв 86, мы можем сказать, что если при делении 60 000 и т. д. на 76 мы получим когда-либо 22 или 60 (поскольку 3×6 и 8×6 оба дают 8), то найдем тем самым решение задачи. Но исследовав первое число, я отверг его и заметил, что если 60 разделить на 76, то получится 0 и 60 в остатке. Следовательно, 8 × 86 = 688 — это и есть второй пример. Можно показать в случае 71, что при делении 10 000 и т. д. на 61 получается в остатке 42 (7 × 61 = 427) и очень длинное частное, приведенное в начале этого раздела, с добавленной к нему 7.

Другие множители не приводят к решению, так что 83, 86 и 71 — три единственных возможных множителя. Те, кто хорошо знаком с принципом рекуррентных десятичных дробей (которого я немного касаюсь в следующей задаче), поймут условия, при которых остатки повторяются после некоторых периодов, и обнаружат, что лишь в двух случаях из трех придется проводить длинные выкладки. Ясно также, что для каждого множителя существует неограниченное число множимых.

83.Решение таково. Поместите на ленточку следующее довольно длинное число:

0212765957446808510638297872340425531914893617.

Его можно умножить на любое число до 46 включительно, и при этом на кольце получится та же самая последовательность цифр. Исходное число можно умножать на любое число до 16 включительно. Я возьму в качестве предела 9, дабы не сбить читателей со следа. Суть дела в том, что эти два числа представляют собой просто числа в десятичном разложении соответственно и 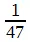. Умножьте первое число на 17, а второе на 47, и вы получите сплошные девятки.

Записывая обычную дробь, скажем, , в десятичном виде, мы действуем следующим образом: добавляем к делимому столько нулей, сколько нам потребуется, до тех пор, пока остаток не станет равным нулю или пока не получим столько знаков, сколько потребуется, ибо каждая дополнительная цифра в бесконечном десятичном разложении приближает нас все ближе и ближе к точному значению.

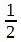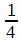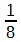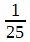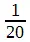Далее: поскольку все степени 10 могут содержать кратные 2 и 5, то отсюда следует, что десятичное разложение никогда не оборвется, если знаменатель вашей обыкновенной дроби содержит какой-либо множитель, отличный от этих двух чисел. Так, , и — приводят к конечным десятичным дробям 0,5, 0,25 и 0,125; и дают 0,2 и 0,4; и приводят к 0,1 и 0,05, ибо в этих случаях знаменатели состоят из кратных 2 и 5. Однако, если вы захотите записать в десятичном виде 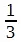, 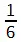или , то никогда не доберетесь до конца, а получите дроби 0,3333 и т.д., 0,166666 и т. д. и 0,142857142857142857 и т. д., где в первом случае 3 повторяется до бесконечности, во втором случае повторяется 6, а в третьем случае мы получаем период 142857.

В случае 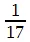(в «Задаче с ленточкой») мы получим повторяющийся период 0,0588235294117647.

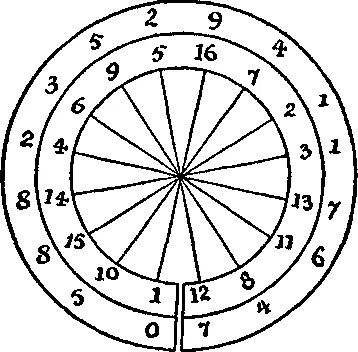
Далее, в приведенных выше выкладках последовательные остатки равны 1, 10, 15, 14, 4, 6, 9 и т. д.; именно эти числа я изобразил на внутреннем круге на рисунке. Можно заметить, что каждое число от 1 до 16 встречается один раз и что если мы умножим наше «ленточное» число на любое из чисел внутреннего круга, то положение последнего точно указывает на начало произведения. Так, если мы умножим наше число на 4, то получим 235 и т. д., если мы умножим его на 6, то получим 352 и т. д. Следовательно, мы можем умножать исходное число на любое число от 1 до 16 и получить при этом желаемый результат.

Суть головоломки состоит в следующем. Любое простое число, за исключением 2 и 5, которые являются делителями 10, делит без остатка любое число, состоящее из девяток, количество которых на I меньше данного простого числа. Например, 999 999 (6 девяток) делится на 7, 16 девяток делятся на 17, 18 девяток — на 19 и т. д. Это будет справедливо всегда, хотя порой достаточно и меньшего числа девяток; например, 9 делится на 3, 99 делится на 11, 999 999 — на 13, и здесь наше «ленточное» правило для последовательных чисел не работает и действует иной закон. Следовательно, поскольку 0 и 7 на концах ленточки нельзя перемещать на другие места, мы должны искать дробь с простым знаменателем, оканчивающимся на 7, что приводит к полному периоду. Мы берем 37 и обнаруживаем, что соответствующий период слишком мал, 0,027, ибо 37 делит 999; следовательно, это число не годится. Затем мы берем 47 и находим, что его полный период совпадает с 46-значным числом, приведенным в начале данного раздела.