Рауль Ибаньес - Мир математики: т.6 Четвертое измерение. Является ли наш мир тенью другой Вселенной?

В упрощенном виде траектории движения муравьев являются одномерными пространствами, так как насекомые движутся по кривым линиям в обе стороны.

Муравьи движутся так, потому что они следуют по запахам феромонов, оставленным другими муравьями. Однако первый муравей (тот, что проложил путь) мог двигаться во всех направлениях. Если мы выпустим муравья на поверхность стола, мы увидим, что он ползает вперед и назад, а также вправо и влево и под любым углом к этим направлениям. Поверхность стола представляет собой двумерное пространство, другими словами, она имеет две степени свободы.

Муравей-первопроходец на поверхности стола с двумя степенями свободы будет двигаться не только вперед и назад, но и в других направлениях.

Этот муравей имеет такую же свободу передвижения, как и Квадрат, живущий во Флатландии. Корабль на поверхности моря и альпинист на склоне горы также движутся в двумерном пространстве. Положение корабля или альпиниста на поверхности земного шара может быть определено с помощью двух параметров: широты и долготы. Аналогично положение муравья на поверхности стола может быть установлено с помощью расстояний от обеих сторон стола.

Если вместо корабля мы рассмотрим подводную лодку, мы добавим возможность перемещения вверх и вниз на конкретную глубину. Точно так же вертолет может подниматься на разную высоту в воздухе. Следовательно, и вертолет, и подводная лодка имеют три степени свободы. Это и есть наше естественное трехмерное пространство.

Если вертолет летает, например, в определенное время каждый день, мы можем добавить еще одну степень свободы — время, хотя в этом измерении мы можем двигаться только вперед, по крайней мере, таково наше восприятие времени. Наша жизнь, таким образом, протекает в четырехмерном пространстве-времени и поэтому может быть задана с помощью четырех координат.

При формулировании понятия степени свободы мы уже видели, что для определения положения в пространстве нам нужны не только числовые значения, но и количество измерений пространства. В примере с вертолетом, движущимся в трехмерном пространстве, GPS определяет его положение с помощью трех чисел — широты, долготы и высоты по отношению к уровню моря — и таким образом использует математическое понятие размерностей в виде набора координат, другими словами, группы чисел.

Возьмем теперь пример с поездом. Представьте себе железнодорожный путь, соединяющий два города с центральной станцией, которая контролирует движение поездов. Положение каждого поезда может быть определено как расстояние от станции в одном или другом направлении (чтобы различать направления, мы обозначим одно знаком плюс, а другое — знаком минус). Следовательно, для определения положения поезда будет достаточно одной координаты (x 1). Пространство всевозможных положений поезда может быть отождествлено с одномерным пространством координат, задаваемых всевозможными значениями х 1.

Аналогичным образом с помощью одного числа можно задать рост каждого члена семьи. Эти значения в некоторых домах можно увидеть на косяке двери, который таким образом становится графическим представлением одномерного пространства всевозможных значений роста.

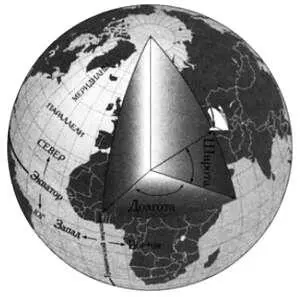
Точное местоположение любого судна в любом океане Земли можно определить с помощью двух чисел — широты и долготы.

Двумя числами (х 1— долгота, х 2 — широта) мы можем описать положение любого места на земной поверхности, которая является двумерным пространством. Более абстрактным примером двумерного пространства будет «пространство», образованное рамками для фотографий, заданными двумя размерами — длиной и шириной. В этом пространстве точкой с координатами (29, 35) является рамка, длина которой 29 см, а ширина — 35 см.

Аналогично, если мы измерим рост и вес членов некой семьи, эти измерения также будут точками в двумерном пространстве, заданными парой измеренных значений. Однако на дверном косяке нельзя будет изобразить эти точки, нам потребуется для этого вся стена. Вот почему ни одна семья не отмечает эти данные таким образом! Стена была бы представлением координатной плоскости. Мы бы отмечали рост по вертикали, а вес — по горизонтали. Тогда пара чисел для каждого члена семьи изображалась бы точкой на стене.

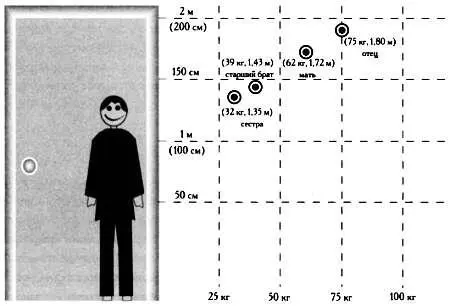
Стена кухни представляет собой координатную плоскость, дверной косяк является осью роста, а плинтус — осью веса. Четыре точки соответствуют четырем парам чисел — росту и весу каждого члена семьи.

* * *

МУХА ДЕКАРТА

Французский математик Рене Декарт(1596–1650) ввел понятие координатной плоскости, а также аналитической геометрии в своей работе «Геометрия», опубликованной в качестве приложения к книге «Рассуждение о методе». По одной из легенд, идея декартовой плоскости пришла к нему в голову, когда он думал о движении мухи по потолку спальни. Декарт понял, что положение мухи может быть задано расстояниями от двух стен. Таким образом, Декарт добавил координаты — алгебраический инструмент — к плоскости Евклида, которая, в свою очередь, находится в некотором геометрическом пространстве. Хотя в наше время координаты могут показаться простым понятием, в то время это было очень трудно воспринять даже Исааку Ньютону (1643–1727), который испытывал сложности при чтении работ Декарта.

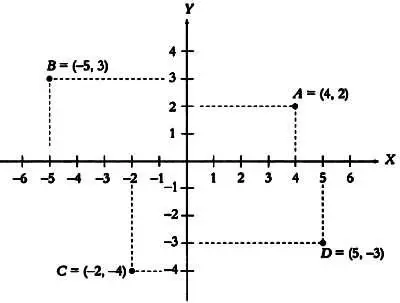
Координатная плоскость с точками А= (4, 2), В= (-5, 3), С= (-2, -4) и D= (5, -3).

* * *

Трехмерное координатное пространство задается тройками чисел (х 1, х 2, х 3). Как уже говорилось, положение вертолета определяется тремя числами — широтой, долготой и высотой. Аналогично более абстрактным примером будет пространство, содержащее картонные коробки, определенные их длиной, шириной и высотой.

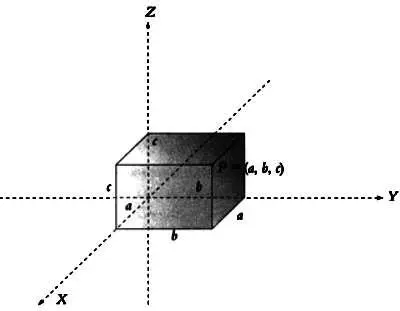
Коробка, изображенная в трехмерном координатном пространстве. Координаты точки ( а, Ь, с) определяют размеры коробки длиной а, шириной b и высотой с.