Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

Американский аукцион проводится по правилам английского, однако его торги закрыты, и один участник может подать заявку лишь один раз.

Также существуют аукционы покупателя, их обычно проводят государственные учреждения, закупающие какие-либо товары или услуги. На этих аукционах предложения подаются в закрытых конвертах, побеждает тот, чья цена будет наименьшей. С этим аукционом схож тендер, в котором победитель определяется на основании не только цены, но и с учетом других факторов.

Сегодня существует множество разновидностей аукционов в зависимости от отрасли, вида товара и других условий: таможенные аукционы, на которых распродаются конфискованные товары, аукционы недвижимости, где финансовые учреждения реализуют имущество, изъятое за долги, публичные торги, интернет-аукционы, проводимые в электронной форме, аукционы, на которых выставляются монеты, произведения искусства, антиквариат и т. д.

Аукцион — это очень прозрачный способ формирования цены и организации рынка, поскольку спрос и предложение на нем ничем не ограничены. Такая форма торговли часто используется на довольно сложных рынках, например валютных, так как аукционы являются очень эффективным средством контроля обмена валют, ассигнования государственных ценных бумаг, казначейских векселей и ценных бумаг с фиксированной доходностью. На рынке ценных бумаг биржи используют аукционы для фиксации котировок на момент начала торгов или на момент закрытия биржевых сессий.

На этой английской карикатуре 1819 года изображается аукцион, на котором Георг IV продал вещи недавно умершей матери.

Проведем исследование рынка на следующем примере: по оценкам, чистящее средство некой марки используют 26 % семей. Была сформирована выборка из 12 семей, которым задали вопрос, какую марку чистящего средства они используют. Нужно определить, какова вероятность того, что в этой выборке от 6 до 9 семей используют чистящее средство рассматриваемой марки. Анализируемая переменная может принимать одно из двух возможных значений («да, используется» и «нет, не используется»), вероятности которых соответственно равны 26 % и 74 % (74 = 100—26).

С помощью законов комбинаторики можно показать, что вероятность РВ(k) того, что в выборке из nсемей kбудут использовать рассматриваемое чистящее средство, равна где р= 0,26 и (1 — р) = 1–0,26 = 0,74. Эта формула соответствует так называемому биномиальному закону распределения вероятностей, выведенному Якобом Бернулли в XVII веке. В свою очередь, указывает число различных сочетаний из kэлементов в группе из n объектов.

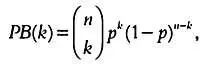
где р= 0,26 и (1 — р) = 1–0,26 = 0,74. Эта формула соответствует так называемому биномиальному закону распределения вероятностей, выведенному Якобом Бернулли в XVII веке. В свою очередь,

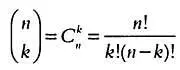
указывает число различных сочетаний из kэлементов в группе из nобъектов.

* * *

РАЗЛИЧНЫЕ СПОСОБЫ ГРУППИРОВКИ ОБЪЕКТОВ

Сочетаниями из nобъектов по k(где k< n) называются все группы из kобъектов; две группы считаются различными, если они отличаются по меньшей мере одним объектом, при этом порядок объектов в группах не имеет значения. Так, число сочетаний (групп) из четырех объектов по 3 обозначается С 3 4и вычисляется по следующей формуле:

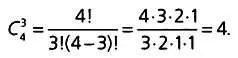
Всего можно составить четыре различные группы. Так, если в качестве четырех исходных элементов мы рассмотрим буквы А, В, С, D, то искомыми четырьмя сочетаниями будут AВС, ABD, ACD, BCD. Существуют другие типы группировки объектов, которые широко используются в дискретной математике, к ним относятся размещения и перестановки.

Размещение из nобъектов по m A n m определяется так: две группы считаются различными, если они отличаются хотя бы одним элементом или же их элементы расположены в разном порядке. Все возможные размещения из четырех элементов ( р, q, r, s) по 3 таковы:

pqr, pqs, prq, psq, prs, psr,

qrp, qpr, qps, qsp, qrs, qsr,

rps, rsp, rpq, rqp, rsq, rqs,

spq, sqp, sqr, srq, spr, srp.

Число размещений вычисляется по формуле A n m= m∙( m— 1)∙( m— 2)…( m— n+ 1). В нашем случае число размещений равно

V 3 4= 4(4— 1)… (4— 3+ 1)= 4∙ 3∙ 2= 24.

Перестановки — это размещения, содержащие все исходные элементы, то есть размещения при m = n. Перестановками из трех элементов ( М, N, Р) являются размещения из 3 по 3. Все возможные перестановки таковы: MNP, MPN, NMP, NPM, PMN, PNM. Число перестановок вычисляется по формуле

Р n = n(n— 1)(n— 2)… (n— n+ 1)= n(n— 1)(n— 2)… 3∙2∙1= n!

В нашем случае Р 3 = 3(3— 1)(3— 2)= 3! = 6.

* * *

Вероятность того, что произойдет одно или несколько возможных событий, равняется сумме вероятностей отдельных событий, если они являются независимыми (то есть не могут произойти одновременно).

В нашем примере вероятность того, что шесть опрошенных используют определенное чистящее средство, равна

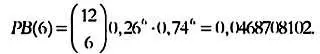
Использовав эту формулу, рассчитаем с помощью Excel таблицу значений от РВ(1)до РВ(12).

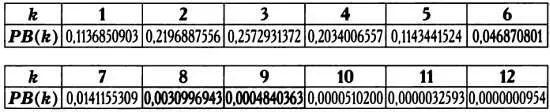
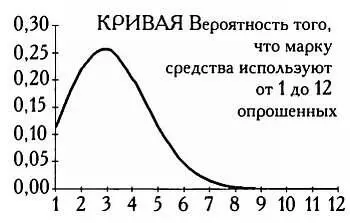
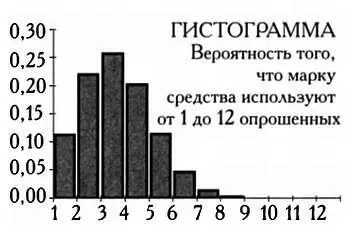
Распределение вероятностей передается графически двумя способами: справа оно представлено на гистограмме, слева — с помощью графика непрерывной функции

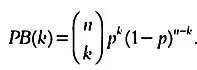
Искомая вероятность того, что рассматриваемую марку средства используют от 6 до 9 опрошенных, равна