Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

РВ(6 < х< 9) = РВ (6)+ РВ (7)+ РВ (8)+ РВ (9)=

= 0,0468708102 + 0,0141155039+ 0,0030996943 + 0,0004840363 = 0,0645700627 = 6,46 %

Средняя величина и среднеквадратическое отклонение для биномиального распределения рассчитываются по формулам:

среднее = μ= n∙ p; среднеквадратическое отклонение = σ =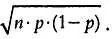

В нашем случае

среднее μ= р = 12∙0,24 = 2,88; среднеквадратическое отклонение = σ = 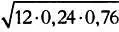= 1,479.

Биномиальное распределение — это распределение вероятностей, график которого при больших объемах выборки стремится к графику нормального распределения.

Кривая биномиального распределения слегка асимметрична по сравнению с кривой нормального распределения, которая полностью симметрична.

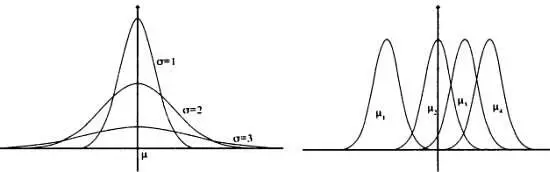
Слева — графики, описывающие три нормальных распределения с одинаковой средней μ и среднеквадратическим отклонением σ= 1; σ= 2; σ= 3. Справа — графики, описывающие три нормальных распределения с одинаковым среднеквадратическим отклонением σ= 1 передними μ 1, μ 2, μ 3, μ 4.

Статистики и экономисты должны уметь работать с широким спектром распределений вероятности. Каждой конкретной ситуации, в которой встречаются случайные величины (переменные, значения которых невозможно спрогнозировать), соответствует определенное распределение вероятностей (функция распределения).

Некоторые распределения вероятностей описывают экономические и социальные явления. Ситуации, когда изучаемая переменная является дискретной (принимает только целые значения или значения «да»/«нет»), адекватно описываются биномиальным распределением. При непрерывных переменных во многих случаях применяется нормальное распределение, или кривая Гаусса.

Живительная математическая теорема, называемая «центральной предельной теоремой», гласит, что на очень больших генеральных совокупностях (при анализе множества деталей, изготовленных на станке, множества избирателей в стране, роста, веса, психологических характеристик людей, поведения групп людей и т. д.) рассматриваемые значения стремятся к нормальному распределению, следовательно, средние значения на выборках, взятых из этой совокупности, также подчиняются нормальному закону и совпадают со средними по всей совокупности. Среднеквадратическое отклонение на выборках также подчиняется нормальному закону и равняется среднеквадратическому отклонению генеральной совокупности.

Центральная предельная теорема является основным связующим звеном между значениями на выборке (несколько объектов) и значениями на большой генеральной совокупности (множество объектов) и показывает, насколько большое значение имеет нормальное распределение вероятности в статистических исследованиях.

По данным периодически проводимых опросов активного населения можно определить параметры всего населения страны с определенной погрешностью, которая описывается доверительным интервалом, о чем мы уже говорили выше.

Вероятность P(z)возникновения события zвычисляется как площадь, ограниченная графиком функции распределения и осью ОХ. Поэтому нет смысла говорить о Р(0,45), так как, во-первых, в связи с погрешностями измерения, неизбежными для любого инструмента, можно говорить лишь об определенном интервале, во-вторых, потому что площадь полученной области будет равна 0.

* * *

СТАНДАРТИЗОВАННОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Стандартизованное нормальное распределение — это упрощенное нормальное распределение изучаемого параметра или переменной. Все значения х iизучаемой переменной меняются: из них вычитается среднее значение i, после чего результат делится на среднеквадратическое отклонение σ. Стандартизованная переменная обозначается буквой z.

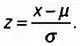
Таким образом, центральным значением множества х i становится не μ , а 0. При делении на σраспределение становится стандартизованным, среднеквадратическое отклонение принимает значение σ = 1. Таким образом, одно и то же распределение (один и тот же график, одну и ту же функцию и одну и ту же таблицу значений) можно использовать для любого нормального распределения после замены переменной, а благодаря этой замене при анализе любого нормального распределения можно использовать одну и ту же таблицу значений.

При переходе к новой переменной (от х к z) все распределения статистических переменных, подчиняющихся нормальному закону, определяются одной и той же функцией распределения (так 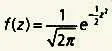при среднем значении, равном 0, и среднеквадратическом отклонении, равном 1.

* * *

При изучении непрерывных статистических переменных имеет смысл говорить только о вероятности попадания значения z на определенный интервал .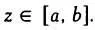

Тогда площадь, ограниченная графиком, есть интеграл от функции плотности:

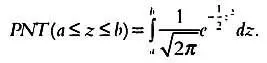
Также можно говорить о вероятности того, что величина z будет не больше определенного значения, то есть будет принадлежать открытому интервалу [ 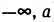]. Эта вероятность рассчитывается так:

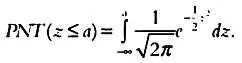
В обоих случаях интеграл позволяет найти необходимую площадь.

Графически вероятность того, что значение zбудет меньше или равно а, изображается областью, выделенной серым цветом на следующем графике, и вычисляется с помощью интеграла:

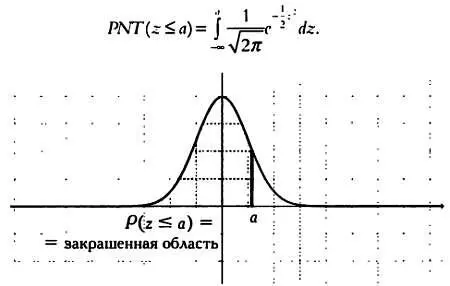
Значение этого интеграла можно вычислить только с помощью методов аппроксимации. С их применением были составлены таблицы распределения вероятностей для стандартизованного нормального закона распределения, позволяющие выполнить любое статистическое исследование, в котором фигурирует нормальное распределение. Эти таблицы можно найти в любой книге по основам статистики, и они позволяют вычислить следующие вероятности: