Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

Одна и та же валюта может обесцениваться по отношению к одним и одновременно расти в цене по отношению к другим валютам. Происходит это из-за того, что, в дополнение к валютным колебаниям, в этих странах меняются индексы цен.

Так, например, если в стране 1 зарегистрирован рост цен р 1больший, чем рост цен р 2в стране 2, обменный курс валют этих двух стран будет изменяться в зависимости от изменения индексов цен в этих двух странах. Если обменный курс валют этих стран равен E, он будет меняться в зависимости от относительного изменения роста цен р 1и р 2, а именно:

Если цены в стране 1 увеличились больше, чем в стране 2, то обменный курс возрастет, то есть валюта страны 1 обесценится. И наоборот, если цены в стране 2 увеличатся больше, чем в стране 1, валюта страны 1 подорожает по отношению к валюте страны 2.

* * *

ПАРИТЕТ ПОКУПАТЕЛЬНОЙ СПОСОБНОСТИ И СТОИМОСТЬ ВАЛЮТ

Чтобы ответить на вопрос, почему одни валюты стоят больше, чем другие, введем еще одно понятие: паритет покупательной способности одной валюты по отношению к другой. На один доллар можно приобрести определенный набор продуктов, однако за эквивалент одного доллара в другой валюте по текущему обменному курсу можно приобрести больше или меньше продуктов.

Подумайте, можно ли купить за 69 евроцентов тот же набор продуктов, что и за один доллар?

Или за 69 евро — в сто раз больше продуктов, чем количество, купленное за один доллар, то есть столько же, сколько можно купить за 100 долларов? Очевидно, что если доллар обесценивается на 10,4 % по отношению к евро, то чтобы купить набор продуктов стоимостью в один доллар, потребуется всего 62,5 евроцента, а не 69 евроцентов, как раньше.

Например, если мы покупаем фотоаппарат, который в США стоит 150 долларов при обменном курсе $1- €0,69, то его стоимость составит €0,69/$ 1∙$150 = 103,50 евро.

Если доллар обесценивается по отношению к евро на 10,4 % и обменный курс снижается до $1 = €0,625 (или €1 = $1,6), то в этом случае фотоаппарат станет для нас дешевле, если мы будем платить в евро: €0,625/$1∙$150 = 93,75 евро.

Может случиться так, что евро обесценится по отношению к доллару (или, что аналогично, доллар повысится в цене по отношению к евро), и его курс станет равным $1,25 за €1 ($1 = €0,80).

В этом случае фотоаппарат обойдется нам дороже, чем европейским покупателям: €0,80/$1∙$150 = 120 евро.

Поэтому когда страна обесценивает свою валюту по отношению к валюте другой страны, экспортируемые ею товары оказываются за границей дешевле, а товары, импортируемые этой страной, дорожают. В этом случае говорят, что покупательная способность валюты снижается.

* * *

С другой стороны, условия торговли определяются как отношение средних цен экспорта к средним ценам импорта, то есть:

Чем лучше условия торговли в стране, тем больше у нее преимуществ при международной торговле: хорошие условия торговли означают, что страна продает товары по высоким ценам, а взамен получает намного больше импортных товаров по более низким ценам. В международной торговле все страны стремятся получить сравнительное преимущество, то есть хотят экспортировать и импортировать определенные товары при благоприятных для себя условиях торговли.

Курсы различных валют являются следствием сделок, совершаемых на финансовых рынках и определяемых потребностями в международных платежах, которые испытывают различные учреждения: коммерческие и центральные банки, транснациональные корпорации, финансовые институты (инвестиционные фонды, пенсионные фонды, страховые компании и т. д.). Наибольшим спросом пользуются валюты, которые чаще всего применяются в международных расчетах. Как правило, это валюты стран с наиболее сильной экономикой.

Спрос на валюту также определяют базовые процентные ставки в странах с этой валютой, а также ожидания участников рынка относительно ее будущих котировок.

На курсы некоторых валют также влияют решения, принимаемые центральными банками государств для поддержания заниженного курса с целью стимулирования экспорта. Так, США, Китай и Япония поддерживают заниженные курсы своих валют по отношению к евро для стимулирования международной торговли.

Расскажем о простейших правилах арифметики в торговле, которые использовались начиная с эпохи Возрождения и до конца XX века. Первое из них — правило пропорции, позволяющее решать задачи, в которых две переменные прямо пропорциональны друг другу (с увеличением одной увеличивается и другая). Если, например, ростовщик зарабатывает три динара на займе в 50 динаров, сколько он заработает на займе в 120 динаров?

50 динаров ____ 3 динара

120 динаров ___ хдинаров.

Как известно, эта задача решается так:

50/120 = 3/ х

50 х= 120-3

50 х/50 = 120∙3/50

х= 120∙3/50 = 7,20 динара.

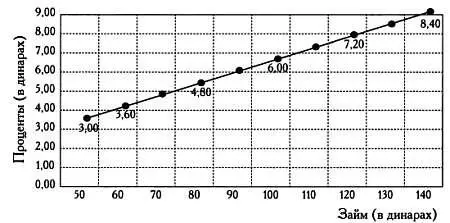
Правило пропорции.

Похожи на них задачи с обратной пропорциональностью. Два каменщика строят стену за 12 дней. Сколько дней понадобится на постройку стены пяти каменщикам?

2 человека ___ 12 дней

5 человек ____ хдней.

Задача решается следующим образом:

2/5 = х/12

2∙12 = 5 х

5 х/5 = 2∙12/5

х= 2∙12/5 = 4,80 дня = 4 дня 19 часов 12 минут.

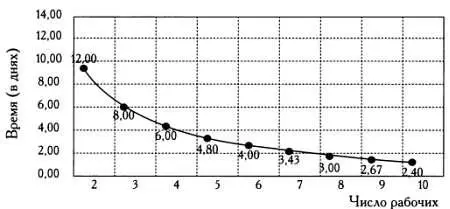
Второй вариант использования правила пропорции.

Наконец, правило пропорции применимо и для решения более сложных задач: если 40 маляров, работая по 8 часов в день, красят 320 метров забора за 10 дней, то за сколько дней 55 маляров покрасят 440 метров такого же забора, если будут работать по 6 часов в день?

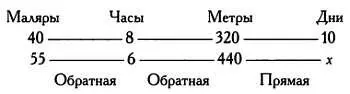
Задача решается следующим образом:

10/ х= 55/40∙6/8∙320/440

х= 10∙440/320∙8/6∙40/55 = 13,3 дня = 13 дней 8 часов.

Греческая буква Σ(заглавная сигма) очень часто используется в математических формулах экономической теории и обозначает сумму слагаемых. Например, для обозначения суммы x 1 + х 2+ х 3 + х 4 можно использовать выражение Σ 4 i=1x i

Знак Σперед х i означает, что нужно сложить все значения х. Числа, указанные под буквой Σи над ней, обозначают границы суммы, то есть наибольшее и наименьшее значение индекса, которое используется при сложении.