Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Рис. 45

Рис. 46

В трактате «О перспективе» (середина 1470 годов – 1480 годы) содержится много отсылок к «Началам» и «Оптике» Евклида, поскольку Пьеро делла Франческа решил доказать, что техника передачи перспективы в живописи полностью основана на математических и физических свойствах визуальной перспективы. На картинах самого художника перспектива представляет собой просторное вместилище, находящееся в полном соответствии с геометрическими свойствами заключенных в нем фигур. По сути дела, для Пьеро сама живопись в первую очередь сводилась к «показу на плоскости тел уменьшенного или увеличенного размера». Такой подход прекрасно виден на примере «Бичевания» (рис. 45 и 47): это одна из немногих картин эпохи Возрождения, где перспектива выстроена и проработана весьма тщательно. Как пишет современный художник Дэвид Хокни в своей книге «Тайное знание» ( David Hockney . Secret Knowledge, 2001), Пьеро пишет фигуры «такими, какими, по его убеждению, они должны быть, а не такими, какими он их видит».

По случаю пятисотой годовщины со дня смерти Пьеро, ученые Лаура Джеатти из Римского университета и Лучано Фортунати из Национального совета по исследованиям в Пизе проделали подробнейший анализ «Бичевания» c помощью компьютера. Они оцифровали всю картину, определили координаты всех точек, перемерили все расстояния и составили полный анализ перспективы на основе алгебраических вычислений. Это позволило им точно определить местоположение «точки схода», где пересекаются все линии, уходящие к горизонту от зрителя (рис. 47), благодаря чему Пьеро и сумел добиться «глубины», которая производит такое сильное впечатление.

Рис. 47

Книга Пьеро о перспективе, отличающаяся ясностью изложения, стала стандартным руководством для художников, пытавшихся рисовать плоские фигуры и геометрические тела, а те ее разделы, которые не перегружены математикой (и более понятны), вошли в большинство последующих работ по перспективе. Вазари утверждает, что Пьеро получил солидное математическое образование и поэтому «лучше любого другого геометра понимал, как лучше всего проводить круги в правильных телах, и именно он пролил свет на эти вопросы» ( здесь и далее пер. А. Габричевского и А. Бенедиктова ). Примером того, как тщательно Пьеро разработал метод рисования правильного пятиугольника в перспективе, может служить рис. 48.

И в «Трактате о счетах», и в «Книжице о пяти правильных многогранниках» Пьеро ставит (и решает) множество задач с участием пятиугольника и пяти платоновых тел. Он вычисляет длины сторон и диагоналей, площади и объемы. Многие решения опираются и на золотое сечение, а некоторые приемы Пьеро свидетельствуют о его изобретательности и оригинальности мышления.

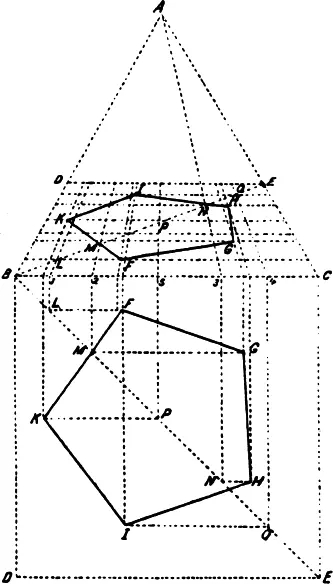
Рис. 48

Пьеро, как и его предшественник Фибоначчи, написал «Трактат о счетах» в основном ради того, чтобы снабдить своих современников-дельцов арифметическими «рецептами» и геометрическими правилами. В тогдашнем мире коммерции не было ни унифицированной системы мер и весов, ни даже соглашений о размерах и формах емкостей, так что без умения вычислять объем фигур было никак не обойтись. Однако математическая любознательность выводила Пьеро далеко за рамки тем, сводившихся к повседневным нуждам. Поэтому в его книгах мы находим и «бесполезные» задачи – например, вычисление длины ребра октаэдра, вписанного в куб, или диаметра пяти маленьких кругов, вписанных в круг большего диаметра (рис. 49). Для решения последней задачи используется правильный пятиугольник, а следовательно, и золотое сечение.

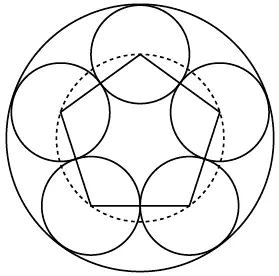
Рис. 49

Алгебраические изыскания Пьеро в основном вошли в книгу, которую выпустил в свет Лука Пачоли (1445–1517) под названием « Summa de arithmetica, geometria, proportioni et proportionalita » («Свод познаний в арифметике, геометрии, пропорциях и пропорциональности»). Труды Пьеро по многогранникам, написанные на латыни, перевел на итальянский тот же Лука Пачоли – и опять же включил (ну, или, выражаясь не столь деликатно, попросту украл) в свою знаменитую книгу о золотом сечении под названием «О божественной пропорции» (« Divina Proportione »).

Кто же он был, этот полный противоречий математик Лука Пачоли? Величайший плагиатор в истории математики – или все же великий популяризатор математической науки?

Лука Пачоли родился в 1445 году в том же тосканском городке Борго Сансеполькро, где родился и держал мастерскую Пьеро делла Франческа. Более того, начальное образование Лука получил именно в мастерской Пьеро. Однако, в отличие от других учеников, выказывавшим способности к живописи – некоторым из них, например, Пьетро Перуджино, суждено было стать великими живописцами, – Лука оказался более склонным к математике. Пьеро и Пачоли сохраняли дружеские отношения и в дальнейшем: доказательством тому служит то, что Пьеро изобразил Пачоли в виде Св. Петра Веронского (Петра Мученика) на «Алтаре Монтефельтро». Еще сравнительно молодым человеком Пачоли перебрался в Венецию и стал там наставником трех сыновей состоятельного торговца. В Венеции он продолжил математическое образование под руководством математика Доменико Брагадино и написал первую книгу по арифметике.

В 1470 годах Пачоли изучал теологию и постригся в монахи-францисканцы. С тех пор его стало принято называть фра Лука Пачоли. В последующие годы он много путешествовал, преподавал математику в университетах в Перудже, Задаре, Неаполе и Риме. В то время Пачоли, вероятно, некоторое время учил и Гвидобальдо Монтефельтро, которому в 1482 году предстояло стать герцогом Урбинским. Лучший, пожалуй, портрет математика – это картина кисти Якопо де Барбари (1440–1515), изображающая, как Лука Пачоли дает урок геометрии (рис. 50, картина находится в музее Каподимонте в Неаполе). Справа на книге Пачоли « Summa » покоится одно из платоновых тел – додекаэдр. Сам Пачоли во францисканской рясе (тоже похожий на правильный многогранник, если приглядеться) копирует чертеж из XIII книги «Начал» Евклида. Прозрачный многогранник под названием ромбокубоктаэдр (одно из архимедовых тел, многогранник с 26 гранями, 18 из которых – квадраты, а 8 – равносторонние треугольники), висящий в воздухе и наполовину наполненный водой, символизирует чистоту и вечность математики. Художнику удалось с поразительным искусством передать преломление и отражение света в стеклянном многограннике. Личность ученика Пачоли, изображенного на этой картине, стала предметом споров. В частности, предполагают, что этот юноша – сам герцог Гвидобальдо. Английский математик Ник Маккиннон в 1993 году выдвинул интересную гипотезу. В своей статье «Портрет фра Лука Пачоли», опубликованной в « Mathematical Gazette » и основанной на весьма солидных исследованиях, Маккиннон делает вывод, что это портрет великого немецкого живописца Альбрехта Дюрера, которого очень интересовали и геометрия, и перспектива (а к его отношениям с Пачоли мы еще вернемся чуть ниже). И в самом деле, лицо ученика поразительно похоже на автопортрет Дюрера.