Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

* * *

ЭЛЛИПС

Эллипсом называется такая кривая, сумма расстояний от любой точки которой до двух фиксированных точек (так называемых фокусов) является постоянной

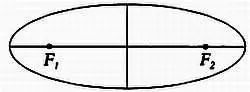
Круг является частным случаем эллипса, когда оба фокуса находятся в одной точке.

* * *

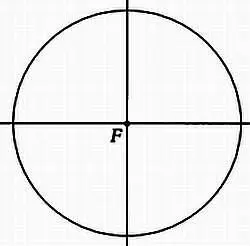
Эллипсоид получается путем вращения эллипса вокруг одной из его осей симметрии. Эллипсоид напоминает апельсин или лимон, а также планету Земля. Земля на самом деле является не сферой, а эллипсоидом, так как она приплюснута на полюсах. Однако для простоты мы будем считать земной шар идеальной сферой.

Для того чтобы понять следующий пример, нам придется включить воображение и вспомнить про Гулливера, путешествующего по стране лилипутов. Представим себе, что эти существа живут на поверхности эллипсоида, и им нужно сделать несколько измерений с помощью транспортира.

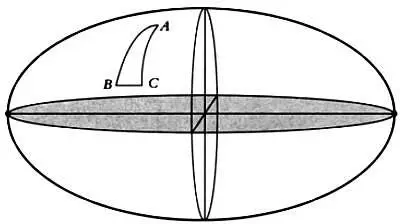
На поверхности эллипсоида нарисован треугольник, вершинами которого являются точки А, В и С . Представьте себе, что два внутренних угла при основании треугольника равны 90° каждый, их измерили живущие на поверхности лилипуты с помощью гигантского транспортира. Верхний угол треугольника будет очень мал, но нам не нужно знать его величину в градусах, так как мы уже видим, что сумма внутренних углов треугольника, нарисованного на поверхности эллипсоида, больше 180°. Это противоречит одной из основных теорем геометрии Евклида: сумма внутренних углов треугольника всегда равна 180°. В эллиптической геометрии все совсем иначе: сумма внутренних углов треугольника, нарисованного на поверхности эллипсоида, всегда будет больше 180°.

В эллиптической геометрии невозможно провести прямую, параллельную данной прямой. Поэтому мы можем сказать, что эллиптическая геометрия отказывается от пятого постулата Евклида, заменяя его другим:

«Через точку вне данной прямой не проходит ни одной прямой, параллельной данной».

Сферическая геометрия является частным случаем геометрии на поверхности эллипсоида. Она очень проста и интуитивно понятна и позволяет довольно легко визуализировать результаты Римана. Поэтому ее стоит рассмотреть в качестве модели эллиптической геометрии.

Сфера — это поверхность, полученная путем вращения окружности вокруг ее диаметра. Плоскость, которая не пересекает сферу, называется внешней по отношению к ней. Если плоскость пересекает сферу только в одной точке, она называется касательной к сфере; в противном случае она будет пересекать сферу по окружности и будет называться секущей плоскостью. Если секущая плоскость проходит через центр сферы, полученное сечение называется большой окружностью.

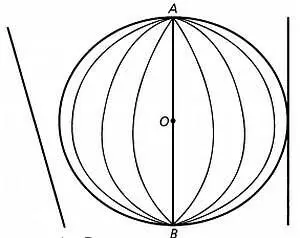
Рассмотрим две точки А и В , такие, что отрезок соединяющий их, проходит через центр сферы О . Эти две точки называются диаметрально противоположными.

В этом случае большие круги, проходящие через диаметр АОВ , называются меридианами, а точки А и В называются полюсами. Для каждой пары таких точек А и В существует один большой круг, перпендикулярный диаметру АОВ , который называется экватором.

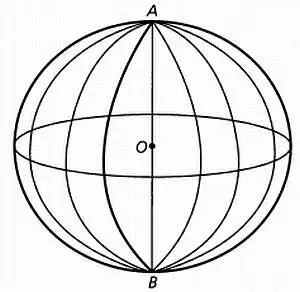
Перпендикуляры к экватору — меридианы — можно наглядно представить. Достаточно рассмотреть очищенный мандарин. Линии, разделяющие дольки, будут пересекаться на полюсах.

Обратите внимание, что два больших круга делят поверхность шара на четыре части.

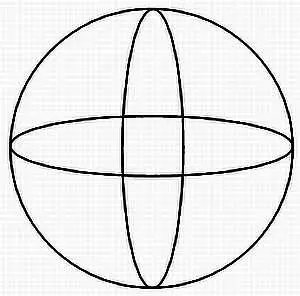
Три больших круга, которые не пересекаются в одной точке, делят поверхность сферы на восемь областей, называемых сферическими треугольниками.

Сферический треугольник также может быть определен как часть поверхности сферы, получаемая в результате пересечения трехгранника и сферы. Дуги на сфере между вершинами А, В и С называются сторонами треугольника.

* * *

ТРЕУГОЛЬНИКИ И ТРЕХГРАННИКИ

Сферический треугольник определяется как часть поверхности сферы, ограниченная тремя большими кругами. Если вершинами такого треугольника являются точки А, В и С , то фигура, определенная точками А, В, С и центром сферы 0, называется трехгранником.

* * *

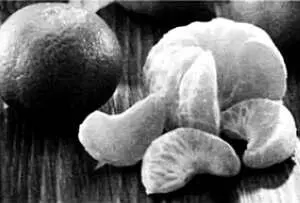
Внешняя поверхность долек мандарина образована двумя меридианами.

Таким образом, на следующем рисунке мы можем ввести такие обозначения: сторону ВС назовем буквой а , сторону АС — Ь , а сторону АВ — с . Буквы А, В и С также часто используются для обозначения внутренних углов сферического треугольника.

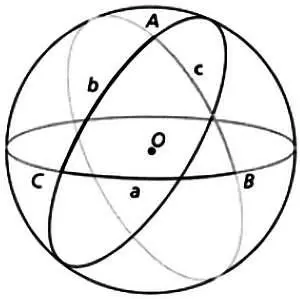
Выполним некоторые вычисления, используя нашу Землю в качестве модели. Для сферы существует несколько полезных формул. Пусть R обозначает радиус Земли, тогда объем ( V ) и площадь ( S ) Земли вычисляются следующим образом:

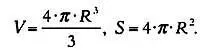
Если радиус Земли взять равным примерно 6350 км, тогда общая площадь Земли составит:

* * *

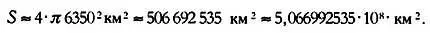
ГРАДУСЫ И РАДИАНЫ

Радиан определяется как величина центрального угла окружности, длина дуги которого равна радиусу окружности. Эта величина составляет примерно 55 градусов 17 минут и 44 секунды. Радиан (часто обозначаемый как рад, rad ) используется в качестве единицы измерения так называемой «круговой меры угла». Если круговая мера угла в радианах равна а , то угол будет равен 180°· а/ πградусов, и наоборот если угол равен G ° , то круговая мера угла составит π· G/ 180радиан.

То есть угол в 360° полной окружности составит 2· πрадиан. В общем случае эти вычисления осуществляются следующим образом.