Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

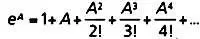
Это выражение для е 4 называется рядом Тейлора, в честь английского математика Брука Тейлора(1685–1713) . Если у вас есть простейший калькулятор с четырьмя основными операциями (сложение, вычитание, умножение и деление), эта формула позволяет посчитать е в любой степени, просто подставив его значение вместо А , чем больше членов ряда будет посчитано, тем выше точность результата. Выражение n! означает произведение n ·( n — 1)·( n — 2)·…·1 и читается как «n факториал». Например: 5! = 5 x 4 x 3 x 2 x 1 = 120.

Если выражение для ряда Тейлора применить к формуле длины гиперболической окружности

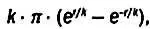
то мы получим:

где последний член очень мал и содержит r в 11-й степени. Если в этом выражении вынести общий множитель С= 2· π ·rза скобки, то мы получим следующую формулу:

* * *

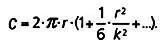
Отношение n/k указывает на различие в свойствах фигур в гиперболической и евклидовой геометриях, где п означает размер фигуры (радиус окружности, длина стороны треугольника). Однако в астрономических масштабах отношение n/k нельзя не учитывать.

На самом деле результаты, о которых мы говорили, служат подтверждением того, что гиперболическая геометрия является обобщением евклидовой геометрии. Лобачевский особенно подчеркивал это свойство своей теории, назвав ее пангеометрией, то есть «универсальной геометрией».

Теорема Пифагора

Всегда полезно взглянуть на известные результаты через призму другой теории. Но именно в теореме Пифагора эффект новых геометрий наиболее заметен. В гиперболической геометрии теорема Пифагора играет столь же важную роль, как и в геометрии Евклида, и, как можно было ожидать, для небольших расстояний она ведет себя так же, как и другие гиперболические объекты. Другими словами, на небольших расстояниях она совпадает с евклидовой версией. Однако при увеличении расстояния ситуация меняется.

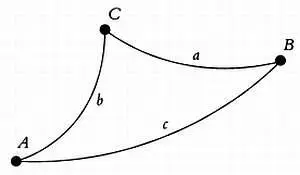
Рассмотрим гиперболический треугольник, стороны которого мы обозначим а, b и с , где с является гипотенузой; вершинами треугольника будут точки А, В и С . Форма гиперболического треугольника отличается от классической:

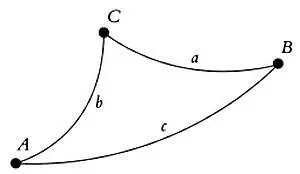
Для этого треугольника справедливо равенство

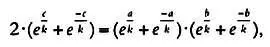
которое может быть переписано в терминах гиперболической геометрии как:

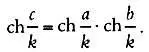
Раскладывая выражение в степенной ряд, как мы это делали для формулы длины окружности, мы получим следующее равенство:

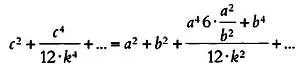
Отсюда видно, что в случае небольших сторон треугольника формула Пифагора остается в силе:

с 2= а 2+ Ь 2,

принимая традиционный вид, как в евклидовой геометрии.

* * *

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

Гиперболические функции называются так потому, что по свойствам они напоминают классические тригонометрические функции. Они таким же образом связаны с гиперболой, как традиционные тригонометрические функции связаны с окружностью.

* * *

Все эти примеры говорят об общем результате, поэтому мы можем утверждать, что параллельные прямые на гиперболической плоскости в малых областях не отличаются от евклидовых параллельных прямых. С другой стороны, в этих вычислениях использовались гиперболические тригонометрические функции — особые аналоги традиционных функций синуса и косинуса. Они называются гиперболическим синусом и гиперболическим косинусом. Добро пожаловать в гиперболическую тригонометрию.

Работая над своими сложными математическими теориями, Бойяи и Лобачевский вывели тригонометрические выражения для гиперболической геометрии. Удивительным является тот факт, что, как и все остальное, они сделали это независимо друг от друга. Это свидетельствует об их гениальности, но также показывает, что результаты, которые они получили, действительно являются правильными.

Соотношения, выведенные Бойяи и Лобачевским, в малых областях могут быть сведены к формулам классической тригонометрии, но в других случаях они характеризуют новые, совершенно неисследованные миры.

Для переменной х гиперболический синус и гиперболический косинус определяются следующим образом:

Аналогично элементарной тригонометрии, гиперболический тангенс определяется следующей формулой:

th x = sh x / ch x

Здесь мы вкратце напомним так называемую теорему синусов.

В треугольнике со сторонами а, b и с и с углами А, В и С

справедливо следующее соотношение:

a / sin A = b / sin В = c / sin С

Аналогичное соотношение можно сформулировать в гиперболической тригонометрии:

sin A / sh a = sin B / sh b = sin С / sh c

Чтобы проверить гиперболические равенства, нужно подставить вместо гиперболических функций их определения:

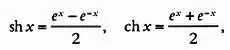
и затем, выполнив соответствующие расчеты, убедиться, что получится один и тот же ответ.