Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

Если πрадиан соответствует 180°, то Rрадиан соответствует G ° , что дает нам следующую пропорцию: π/ 180 = R/ G. Например, сколько радиан имеет угол в 30°? Подставляя в формулу, получим π/ 180 = R/ 30, откуда находим R:

R= (30· π/180 )= π/6 рад.

Мы также можем решить обратную задачу. Сколько градусов имеет угол в π/4 радиан? Подставляя в формулу, получим

π/180 = ( π/4)/ G, откуда находим G:

G= (( π/4)·180)/ π= 45°

* * *

Применим теперь формулу для объема и получим:

V= (4· π·6350 3)/3 = 1,072499199·10 12·км 3

С этими результатами мы можем вычислить площадь октанта, одной восьмой части земной поверхности. Просто разделим значение площади Земли на 8. Это дает нам 63336566,88 км 2.

Как мы видим, каждый октант очерчивает сферический треугольник с углами 90° = π/2 радиан. Обратите внимание, что общая сумма составляет 270° = З π/2 радиан (то есть более чем 180° = πрадиан). Тогда чему будет равна каждая из сторон?

Каждая из сторон представляет собой дугу большого круга. Используя формулу для длины дуги, получим:

( α· R) = ( π/2)·6350 = 9 974,2625 км

Этот же результат можно получить и другим способом: разделить длину большого круга на четыре (напомним, что длина окружности составляет 2πR):

( 2π·6350)/4 = 9974,2625 км.

Ясно, что ту же процедуру можно повторить для Луны, радиус которой равен 1736 км.

* * *

ДЛИНА ДУГИ КРУГОВОГО СЕКТОРА

Для части окружности с центром O и радиусом r , изображенной на рисунке, обозначим α угол, измеряемый, как правило, в радианах, а с — дугу между точками А и B . Тогда длина дуги выражается следующим образом: с= α· r.

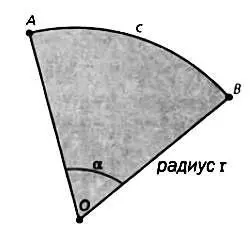
Имея дело с длиной стороны сферического треугольника, мы обычно используем круговую меру угла, которую фактически нужно лишь умножить на радиус.

* * *

Вернемся к нашему общему вопросу. Геодезической линией называется кратчайшая линия, соединяющая две точки на поверхности и сама принадлежащая этой поверхности. На совершенно плоской, то есть евклидовой поверхности, геодезической линией является отрезок. Между двумя точками А и В на сферической поверхности из всех окружностей, проходящих через эти точки и расположенных на этой сфере, геодезической линией является большой круг. Другими словами, геодезическая линия получается путем пересечения сферы плоскостью АОВ . Таким образом, геодезическим отрезком между точками А и В является меньшая из дуг большого круга, проходящего через А и В . Обратите внимание, что случай с этим кругом — единственный, когда А и В не являются диаметрально противоположными точками.

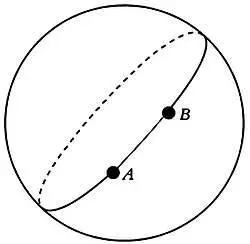
В геометрии на сфере прямыми линиями являются дуги больших кругов. Таким образом, параллельные линии не существуют, так как большие круги всегда пересекаются в диаметрально противоположных точках. Для наглядности достаточно взглянуть на дольки очищенного апельсина.

* * *

ПОВЕРХНОСТЬ ЗЕМЛИ

Является ли единственным кратчайший путь между двумя европейскими столицами, например, между Лондоном и Парижем? Ответ на этот вопрос положителен: существует только одна геодезическая линия, соединяющая эти города. Аналогично, уникален ли маршрут между Северным и Южным полюсами? Здесь ответ отрицательный: существует бесконечное количество геодезических линий, соединяющих эти две точки, так как они диаметрально противоположны.

* * *

Мир сферических треугольников иллюстрирует много математических свойств эллиптической геометрии. Поэтому стоит его рассмотреть подробнее. Для начала рассмотрим на сфере радиуса R сферический треугольник с вершинами А, В, С и сторонами а, Ь, с.

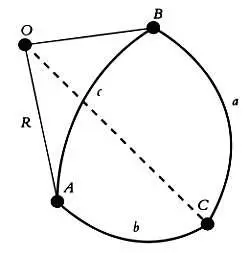
Одним из результатов, о котором мы уже говорили, является тот факт, что сумма углов сферического треугольника больше 180°, или πрадиан, и меньше 360° = 2 πрадиан. То есть

π< A+ В+ С< 2 π.

Таким образом, можно сказать, что сумма сторон сферического треугольника удовлетворяет неравенству:

a + b+ c< 2· π· R.

Величина ( А + В + С — 180°) называется сферическим избытком, так что площадь сферического треугольника S находится по следующей формуле:

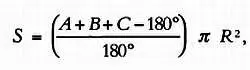
где R — радиус сферы.

Следует отметить, что чем больше площадь треугольника, тем больше сумма его углов. Кроме того, чем больше площадь треугольника, тем больше сферический избыток, и именно поэтому больше значение А + В + С .

В евклидовой геометрии имеется следующий результат: длина окружности радиуса r равна 2 πr. В эллиптической геометрии этот результат выглядит следующим образом: длина окружности радиуса r всегда больше, чем 2 πr.

* * *

ПЛОЩАДЬ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА НА ПОВЕРХНОСТИ ЗЕМЛИ

Давайте решим следующую задачу: какова должна быть площадь сферического треугольника на поверхности Земли, чтобы сумма его углов была больше 180° хотя бы на 1°? По формуле для площади сферического треугольника имеем:

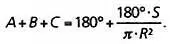
Мы хотим найти значение S , такое что

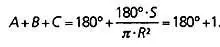
Отсюда получаем

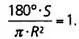
Выражая S и подставляя 6350 км вместо R , имеем

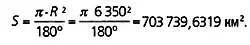
Следовательно, у любого треугольника на поверхности Земли, площадь которого равна или больше 703739,6319 км 2, сумма углов будет превышать 180° по крайней мере на 1°.