Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

Тем не менее практически решил эту задачу не математик, а садовод. И практическое решение математической задачи — это результат математического творчества.

При обрезке деревьев обычно удаляются ветви нижней его трети, и лесничему нужно на глаз определить эту часть дерева. Является ли треть того, что мы видим, третьей частью того, на что мы смотрим? Как правило, это не так:

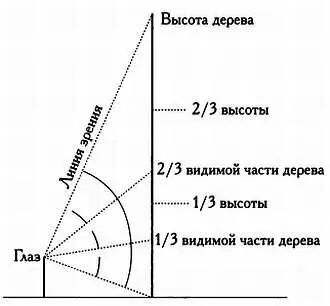
Визуальное и реальное деление предмета на три части совпадают, только когда мы рассматриваем дугу окружности, находясь в ее центре. Как же лесничий решит задачу? Как визуально определить треть предмета, на который он смотрит?

Чаще всего точная высота дерева нам неизвестна. Если А 1 — угол зрения, под которым можно увидеть все дерево, а — уровень глаз, d — расстояние до основания дерева, то угол А 3 определяющий нижнюю треть дерева, вычисляется по формуле:

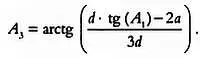
В чем заключается суть вопроса? В том, что видимая величина угла меняется в зависимости от точки, из которой мы смотрим на него. Видимая середина отрезка будет соответствовать его истинной середине только в том случае, если мы будем находиться на серединном перпендикуляре к этому отрезку:

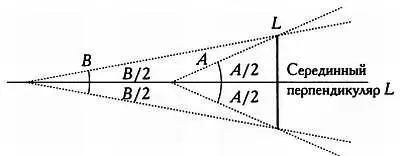
При делении отрезка на три части подобная ситуация невозможна. Если бы она была возможна, то существовала бы точка X плоскости, такая, что при взгляде из нее трети Р 1Р 2, Р 2Р 3 и P 3P 4 отрезка Р 1Р 4 были бы видны под одним и тем же углом (см. рисунок ниже). Следовательно, так как из точки X можно было бы увидеть под одним и тем же углом две половины P 1P 3 точка X должна была бы располагаться на серединном перпендикуляре к отрезку P 1P 3 (то есть на прямой, проходящей через Р 2 и перпендикулярной P 1P 3 ). Это же было бы справедливо для серединного перпендикуляра к отрезку Р 2Р 4 (прямой, проходящей через Р 3 и перпендикулярной Р 2Р 4 ). Таким образом, точка X должна была бы располагаться одновременно на двух серединных перпендикулярах, которые параллельны между собой, так как они перпендикулярны одному и тому же отрезку P 1P 4 , что невозможно:

За исключением случая, когда мы смотрим на дугу окружности, находясь в ее центре, треть того, что мы видим, — вовсе не треть того, на что мы смотрим.

Округление чисел выполняется по следующим правилам: если последний знак десятичной записи числа меньше 5, этот знак заменяется на 0, если же последний знак больше 5, то предыдущий знак увеличивается на единицу:

2,34 ~= 2,3;

2,37 ~= 2,4.

Ошибки округления в одну десятую, сотую или тысячную при работе с большими числами могут быть значительными. Если ошибка в одну сотую евро повторится на 300 миллионах счетов, общее расхождение составит 3 миллиона евро. В бухгалтерском учете подобное недопустимо. При составлении балансов даже сотые доли евро могут повлиять на итоговое значение округленной величины:

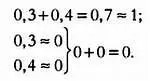
Имеем теорему:

Округленная сумма значений не равна сумме округленных значений.

Это утверждение можно подтвердить с помощью следующих таблиц:

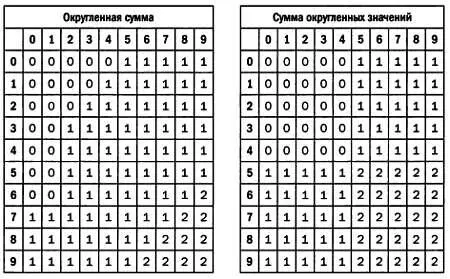
Обратите внимание, с какой частотой в таблицах фигурируют числа 0, 1 и 2:

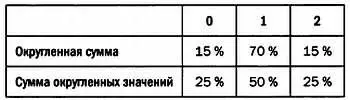
Почему мы не можем определить операцию округления так, чтобы 0, 1 и 2 распределялись более равномерно? Например, так, чтобы каждое из этих чисел фигурировало в таблице примерно в 33,3 % случаев. Эта ситуация представлена ниже: 0, 1 и 2 в таблице встречаются 33, 34 и 33 раза соответственно:

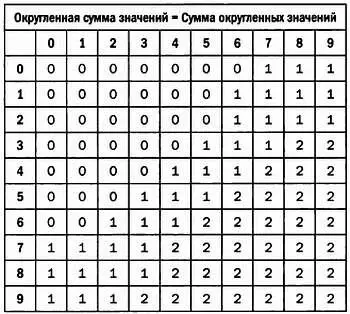
Расположение продуктов в европейских холодильниках можно оптимизировать благодаря стандарту упаковок Gastronorm EN 631 . Все упаковки, разработанные в соответствии с этим стандартом, имеют прямоугольную форму и обозначаются числовым кодом, указывающим соотношение размеров упаковки. Перечень кодов представлен ниже:

2/1 2/3 2/4 2/8 и 1/1 1/2 1/3 1/4 1/6 1/9.

Базовая упаковка обозначается кодом 1/1 и имеет размеры 530 х 265 мм.

Остальные упаковки получаются из базовой так, как показано на иллюстрации.

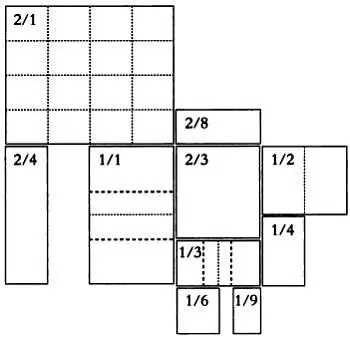
Таким образом, обозначение каждой упаковки выражает отношение ее размера и размера базовой упаковки 1/1:

2/1 = удвоенная упаковка 1/1;

2/4 = четверть 2/1 = половина 1/1;

2/8 = восьмая часть 2/1 = четверть 1/1;

2/3 = две трети 1/1;

1/2 = половина 1/1;

1/3 = треть 1/1;

1/4 = четверть 1/1;

1/6 = половина 1/3;

1/9 = треть 1/3.

Все эти равенства верны с точки зрения математики:

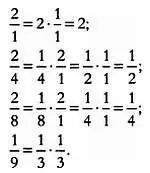
Следовательно, коды стандарта Gastronorm , по сути, представляют собой дроби, четко указывающие соотношение размеров упаковок. Чтобы узнать, скольким упаковкам формата 1/6 равна упаковка формата 2/3, достаточно выполнить деление:

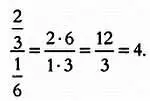
Система Gastronorm подобна игре в тетрис и позволяет заранее рассчитать оптимальное расположение упаковок, например, на полке холодильника, при этом упаковки будут располагаться рядом друг с другом, подобно элементам головоломки.

Многие писатели прошлого и современности очень четко передают математические идеи, объясняют их и сопровождают примерами, что помогает лучше усвоить многие понятия и взглянуть на них по-новому. Чтобы проиллюстрировать это, обратим внимание на два рассказа: один из них принадлежит перу Хорхе Луиса Борхеса, второй — Итало Кальвино.