Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

* * *

ДЖОН НЕПЕР (1550–1617)

Математик Джон Непер создал теорию логарифмов, которые он называл искусственными числами. В его честь были названы неперовы (натуральные) логарифмы. Он очень интересовался богословием: применив математические методы для толкования «Откровений» святого Иоанна Богослова, он вычислил, что конец света наступит в период с 1688 по 1700 год.

* * *

Палочки Непера представляют собой не что иное, как разновидность таблицы умножения. Это десять деревянных палочек квадратного сечения, пронумерованных от 0 до 9. На них отмечены девять промежутков, на которых записаны девять чисел, кратных данному. Разряды двузначных чисел разделены наклонной чертой, как показано на рисунке.

Современная реконструкция палочек Непера.

Чтобы продемонстрировать пример использования этого устройства, рассмотрим умножение числа 35672. Мы выбрали это число, чтобы показать применение всех строк таблицы. Нужно последовательно расположить палочки, соответствующие пяти цифрам этого числа, то есть сначала — палочку под номером 3, затем под номером 5, далее — 6, 7 и 2. Простое наблюдение за положением палочек позволяет увидеть, что в каждом ряду будут записаны результаты умножения 35 672 на все числа от 1 до 9.

Следовательно, чтобы умножить 35 672 на 4, нужно взять числа из четвертого ряда:

1/2 2/0 2/4 2/8 0/8.

Далее нужно сложить соседние числа пар, разделенные наклонной чертой:

1/2 + 2/0 + 2/4 + 2/8 + 0/8.

Получим:

1/4/2/6/8/8.

Таким образом, результат умножения 35672 на 4 равен 142688. Вы можете проверить его правильность вручную или на калькуляторе.

35 672·4 = 142 688.

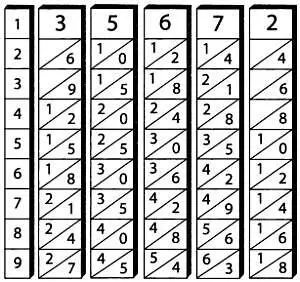
Умножение 35 672 на 4 с помощью палочек Непера.

Умножение многозначных чисел выполняется аналогично современному способу: каждая цифра второго числа последовательно умножается на первое число, после чего полученные результаты складываются. Промежуточные результаты умножения получаются по уже описанной нами схеме. Следует отметить, что все необходимые промежуточные результаты находятся в одной и той же таблице. Например, чтобы умножить 35 672 на 436, нужно выполнить расчеты по описанной нами схеме в рядах 4, 3 и 6. Мы получим несколько чисел, которые нужно записать друг под другом так, чтобы диагональные линии оказались расположены в ряд.

При таком расположении чисел умножение 35 672 на 436 сводится к сложению промежуточных результатов, как показано ниже. Сначала записаны промежуточные результаты умножения, затем суммы пар чисел, разделенных диагональными чертами и, наконец, результат, полученный переносом значений в старший разряд там, где это необходимо.

Выполните эти действия на калькуляторе и убедитесь, что результат абсолютно верен:

35 672·436 = 15 552 992.

Заметьте, что числа в строках соответствуют промежуточным результатам, получаемым при известном нам способе умножения столбиком. Эти промежуточные результаты равны:

Однако палочки Непера использовались не только для умножения. Для деления одного большого числа на другое достаточно расположить палочки на столбцах, соответствующих цифрам делителя. В строках таблицы будут записаны числа, кратные делителю, которые помогут быстрее получить результат деления.

Джон Непер также является автором еще одного важного открытия — логарифмов. Этот шотландский математик обнаружил, что с их помощью можно свести сложные математические операции к более простым. Умножение сводилось к сложению, деление — к вычитанию, возведение в степень — к умножению, извлечение корней — к делению. Это чрезвычайно упростило выполнение сложных расчетов вручную и дало мощный толчок развитию математики.

log( a · b ) = log( а ) + log( b )

log( a / b ) = log( a ) — log( b )

log( a b ) = b · log( a ).

Следовательно, для вычисления произведения а · Ь достаточно вычислить e log( a ) + log( b )

На основе логарифмов была создана логарифмическая линейка — еще одно важнейшее вычислительное устройство. Ее автором был британский математик Уильям Отред(1574–1660) , который впервые стал обозначать умножение знаком X, функции синуса и косинуса — sin и cos соответственно. Этот математик использовал устройство, разработанное Эдмундом Гантером, в котором применялась одна логарифмическая шкала (в логарифмической линейке используются две шкалы). Позднее, в 1859 году, француз Амадей Манхейм представил ряд улучшений, и логарифмическая линейка обрела современный вид.

Портрет Уильяма Отреда, который считается изобретателем логарифмической линейки.

Логарифмические линейки не использовались для сложения и вычитания. Они были более удобны для умножения и деления и применялись преимущественно для выполнения именно этих операций. Более поздние версии позволяли вычислять значения корней, тригонометрических функций, степеней и логарифмов. Однако следует заметить, что точность логарифмической линейки была ограниченной: как правило, использовались три значащие цифры. Однако с помощью более точных линеек, имевших больший размер, достигалась более высокая точность. Требовалось обращать внимание на порядки величин, так как при использовании логарифмической линейки они не учитывались. Логарифмические линейки применялись в качестве средства научных расчетов до 1970-х годов, пока их не вытеснили карманные электронные калькуляторы.

Модель логарифмической линейки 1960-х годов. Этим вычислительным устройствам вскоре пришли на смену калькуляторы.

Первые калькуляторы

Первый электронный карманный калькулятор появился в 1972 году. Это была знаменитая модель Hewlett-Packard НР-35 . Пока что мы рассказывали об эволюции исчисления и средствах его автоматизации, то есть о развитии теоретической базы, на основе которой в итоге был создан карманный калькулятор и впоследствии множество других устройств, без которых мы не можем сегодня представить нашу жизнь.