Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

Устройство арифмометра Шарля Ксавье Тома де Кольмара(вверху) и калькулятора, изобретенного Гэтфридом Лейбницем.

Лейбниц внес важный вклад не только в развитие систем счисления. Этот немецкий философ также является автором значимых трудов по логике. Его работы в этой области были опубликованы посмертно, так как, по всей видимости, Лейбниц был не вполне доволен ими. Заглавие одной из его работ, Post tot logicas nondum Logica qualem desidero scripta est, можно перевести как «После стольких логик та логика, что я сочинил, еще не была написана». Он работал над созданием логического исчисления, которое можно было бы применять к любым научным высказываниям.

В одной из своих работ Лейбниц писал:

« Если нам это удастся, то, когда возникнет противоречие, необходимости в споре между двумя философами будет не более чем между двумя математиками. Будет достаточно взять перья и абак и сказать друг другу: произведем вычисления ».

* * *

ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646–1716)

Немецкий мыслитель Готфрид Вильгельм Лейбниц вместе с Декартом и Спинозой входит в тройку великих рационалистов XVII века. Он был математиком, логиком, философом, геологом, историком и экспертом в юриспруденции. Он также внес огромный вклад в технологию и предвосхитил появление многих понятий в биологии, медицине, психологии и даже информатике. Независимо от Ньютона он создал анализ бесконечно малых. Введенные им обозначения используются и сейчас.

Составить полный перечень его открытий невозможно, поскольку до сих пор не издано полное собрание всех его сочинений, разбросанных по дневникам, письмам и рукописям, некоторые из которых никогда не публиковались. Лейбниц установил соответствие между двоичной системой счисления и сотворением мира: в его математическом представлении космоса, напоминавшем пифагорейское, ноль обозначал пустоту, единица — Бога.

* * *

В этой работе прослеживается влияние Раймунда Луллия: при написании «Рассуждения о комбинаторном искусстве» ( Dissertatio de Arte Combinatoria ) Лейбниц вдохновлялся его «Великим искусством». Для Лейбница даже приближение к божественному знанию должно было достигаться исключительно путем комбинирования основных понятий. Эти основные понятия, которым невозможно дать определение, должны были выражаться на языке математики. На их основе с помощью четких дедуктивных правил должны были выводиться различные истинные высказывания.

Лейбниц считал, что между логикой, математикой и метафизикой существует тесная взаимосвязь. Он был убежден, что его метафизика полностью математическая и что истинную метафизику сложно отличить от истинной логики.

Новые выражения для вычисления числа π

В течение XVII века различные исследователи предпринимали попытки вычислить значение π с помощью бесконечных рядов, следуя путем, который наметил Франсуа Виет. Одним из них был англичанин Джон Валлис(1616–1703) из Оксфордского университета. В своей книге «Арифметика бесконечного», опубликованной в 1633 году, Валлис описал различные выражения для вычисления интегралов и, взяв их за основу, получил следующее выражение для числа π :

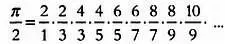
Математик и философ Уильям Броункер(1620–1684) , основатель и первый президент Лондонского королевского общества, путем преобразования этого выражения в 1658 году получил следующую формулу:

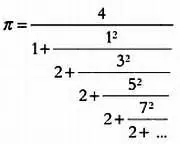
Следующее выражение, известное в Европе, было открыто за ее пределами. Речь идет о формуле Мадхавы из Сангамаграма. Лейбниц повторно открыл ее в 1671 году, использовав разложение в ряд для функции арктангенса, полученное Джеймсом Грегори. Она выглядит так:

π /4 = 1–1/3 + 1/5 — 1/7 + … + (-1) n /(2 n + 1) + …

и выводится из следующего разложения в ряд для арктангенса:

arctg x = х — ( x 3)/3 + ( х 5)/5 — ( х 7)/7 + …

XVIII век остался в истории веком Просвещения. Целью этой книги ни в коей мере не является критика Просвещения, однако нет сомнений в том, что в XVIII веке не было сделано значимых открытий в области исчисления и счета. Возможно, в XVII веке был совершен столь крупный прорыв в науке, что в последующем столетии ученые занимались исключительно изучением уже открытого ранее. Как бы то ни было, вычисления, логика и расчеты числа 71 в этот период следовали по пути, очерченному в XVII веке.

Вычисление числа π в XVIII веке

В XVIII веке было предложено несколько новых выражений для вычисления числа π . Первое из них получил астроном Джон Мэчин(1680–1751) . Оно использовалось для вычисления π в течение нескольких веков, в том числе при компьютерных вычислениях. Использовав формулу Грегори, Лейбница и Мадхавы, Мэчин обнаружил, что угол, арктангенс которого равен 1/5, можно выразить так:

α = arctg(1/5) = (1/5) — ((1/5) 3)/3 + ((1/5) 5)/5 — ((1/5) 7)/7 +…

На основе арктангенса угла (4 α — π /4) он составил ряд, позволяющий вычислить число π , в котором используется функция, обратная котангенсу. В отличие от предыдущих, этот ряд сходился быстрее. С его помощью этому английскому математику удалось верно вычислить 100 знаков числа π . Этот ряд соответствовал следующему выражению:

π /4 = 4·arctg(1/5) — arctg(1/239).

Это выражение можно представить в виде следующего ряда:

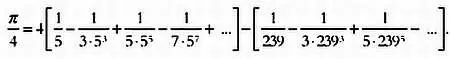
Леонард Эйлер также внес вклад в исследование рядов, позволяющих вычислить число π . С помощью одной из своих формул ему удалось вычислить 20 знаков π менее чем за полчаса.

* * *

ЛЕОНАРД ЭЙЛЕР (1707–1783)

Швейцарский математик и физик Леонард Эйлер прожил большую часть жизни в России и Германии. Он считается ведущим математиком XVIII века и одним из крупнейших математиков всех времен. Он совершил важнейшие открытия в области анализа бесконечно малых и теории графов, а также ввел множество терминов и обозначений современной математики, особенно в области анализа, в частности обозначение функции. Он также совершил важные открытия в механике, гидродинамике, оптике и астрономии. Он был невероятно плодовитым ученым: полное собрание его сочинений насчитывает от 60 до 80 томов.