Хавьер Фресан - Том. 22. Сон разума. Математическая логика и ее парадоксы

— Ранее у вас было немецкое гражданство?

— Нет, австрийское! — поправил чиновника Гёдель.

— Какая разница, в любом случае — страна с проклятым диктатором. К счастью, в Америке это невозможно!

— Совершенно наоборот, — перебил Гёдель. — И я знаю, как это может случиться!

Однако чиновник, которого Альберт Эйнштейн предупредил, что Гёдель отличается от остальных кандидатов, взял нить разговора в свои руки и перешел к рутинным вопросам, сказав: «Не будем умствовать». Примерно в то же самое время некоторые логики начали формировать основы новой теории — деонтической логики, целью которой было избежать противоречий при дополнении существующих законов новыми положениями.

* * *

21 июня 1851 года Адольф Андерсен, лучший шахматист того времени, встретился в одном из старейших ресторанов Лондона с Лионелем Кизерицким, преподавателем шахматного клуба в Париже, и сыгранная ими партия позже была названа бессмертной. Впечатленный стратегией Андерсена, который пожертвовал слоном, ферзем и двумя ладьями, Кизерицкий захотел отправить запись партии в свой шахматный клуб. «Белые: пятая пешка слева передвинута на две клетки вперед. Черные: пешка на той же вертикали ставится перед пятой пешкой белых. Белые: третья пешка справа передвигается на две клетки вперед. Черные: пешка, которой был сделан первый ход, бьет пешку, которой белые совершили последний ход»… Но нет! Запись выглядела вовсе не так. Ее первые символы: е2—е4 е7—е5 f2—f4 е5: f4 …». Вся запись заняла не больше трех строк!

Если бы шахматист использовал первый способ записи, стоимость телеграммы с описанием партии превысила бы стоимость счета в «Кафе де ля Режанс», где сыграть в шахматы можно было за пять франков в час.

Игроки разработали чрезвычайно краткий способ записи ходов. Для этого они, во-первых, применили старинный метод аналитической геометрии Декарта, благодаря которому каждая клетка шахматной доски стала обозначаться двумя координатами: латинской буквой от а до h обозначались вертикали, числами от 1 до 8 — горизонтали. Пешки не обозначались никак, а все остальные фигуры получили обозначения по первым буквам названий (в русской нотации: Кр — король, Ф — ферзь, А — ладья, К — конь, С — слон). Далее нотация пополнилась другими символами: взятие фигуры обозначалось буквой х (в русской нотации — двоеточием), шах — знаком умножения в русской нотации и решеткой (#) — в международной. В этой нотации последовательность символов « е2—е4 е7—е5 f2—f4 е5: f4 » означает: «белые делают ход пешкой на клетку е4 , черные отвечают ходом пешки на е5 . Затем белые делают ход пешкой на f4 , черные проводят взятие этой пешки пешкой, которая находилась на клетке е5 ».

Этот пример подтверждает, насколько удобно использовать системы кодов в различных областях, в том числе за пределами математики, преобразуя сложные выражения в цепочку простых символов. В предыдущей главе вы видели, как свойства натуральных чисел, записанные обычным языком, можно перевести на язык символов, описанный в «Началах математики». Так, аксиома «0 не следует ни за каким натуральным числом» в этой системе преобразуется в формулу 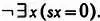Однако Гёделю требовалось сделать еще один шаг вперед: чтобы доказать теорему о неполноте, ему было недостаточно свести арифметику к формулам — требовалось свести любую формулу и даже любое доказательство к единственному числу.

И Гёдель вспомнил, что на семинарах по истории философии, которые он посещал во время учебы в Венском университете, профессор Теодор Гомперц рассказывал об издании Луи Кутюром отредактированных рукописей Лейбница в 1903 году.

Подобно своим гениальным предшественникам, Лейбниц потратил немало сил, чтобы положить конец вавилонскому смешению языков, которым Бог наказал людей за то, что они хотели построить башню высотой до самого неба. Для этого Лейбниц задумал универсальный язык, в котором все человеческие мысли вне зависимости от языка носителя сводились к каталогу первичных идей, каждой из которых ставилось в соответствие простое число. С помощью этой системы можно было найти числа, соответствующие производным идеям так, что всегда было возможным «извлечь базовые обозначения, их составляющие», подобно тому, как из простых чисел образуются составные. Если понятиям «вода» и «неподвижность» поставлены в соответствие, например, числа 3 и 5, то понятие «озеро» (неподвижная вода) можно выразить произведением 3·5. И напротив, если понятие озера обозначается числом 15, мы можем разложить 15 на простые множители, найти в энциклопедии основных идей те, что соответствуют числам 3 и 5, и сделать вывод, что озеро есть не более чем неподвижная вода. Так, чтобы узнать, является ли утверждение вида « А есть В » истинным, достаточно определить, делится ли число, обозначающее В , на число, обозначающее А , и «когда возникнет противоречие, необходимости в споре между двумя философами будет не более, чем между двумя математиками». Эта амбициозная программа Лейбница, открытая спустя двести лет после его смерти, никогда не была реализована, однако она подсказала Гёделю, как можно перевести метаязык на язык арифметики.

Напомним, что простые числа — это числа, которые делятся только на 1 и на самих себя: например, число 5 простое, так как не делится ни на 2, ни на 3, ни на 4, однако 6 не является простым, так как при делении на 2 дает 3. Первыми простыми числами являются 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31. Путем доказательства от противного, которое так не любили интуиционисты, можно установить, что этот перечень простых чисел можно продолжать бесконечно. Большинство усилий физиков второй половины XX века было направлено на определение элементарных частиц, из которых состоит материя и которые нельзя разделить на другие, более мелкие частицы. Математикам же со времен Евклида известно, что элементарными частицами арифметики являются натуральные числа. Действительно, для любого натурального n возможны два варианта: либо n является простым, либо существует число, отличное от 1 и n , которое является делителем этого числа. Если, например, n равно 23, то мы имеем дело с первым случаем, но если n равно 30, то его можно разделить на 2.

Следовательно, исходное число не является простым. Его можно представить в виде произведения: n = а · b (в нашем случае 30 = 2·15). Мы получили два числа, для которых повторим вышеописанные действия: если оба этих числа являются простыми, процесс на этом завершается, но если одно из них не является простым, мы вновь запишем его в виде произведения сомножителей. В нашем примере 2 является простым, однако 15 можно представить в виде произведения 15 = 3·5, таким образом, 30 = 2·3·5. Так как 2, 3 и 5 — простые числа, процесс на этом завершается. В общем случае мы либо находим простой сомножитель, либо найденные нами множители постепенно уменьшаются — это гарантирует, что описанный нами процесс рано или поздно завершится. Таким образом, мы доказали основную теорему арифметики, которая гласит, что любое число можно представить в виде произведения простых множителей, которые могут повторяться. Пример: 77220 = 2·2·3 x 3·3·5·11·13. В этом случае используется сокращенная запись: 77 220 = 2 2· З 3х 5·11·13, где показатели степеней указывают, сколько раз повторяется каждый сомножитель.