Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

Нам потребуется теорема Пифагора, согласно которой квадрат гипотенузы равен сумме квадратов катетов, то есть если h — гипотенуза, а и Ь — катеты, то:

h 2= a 2 + Ь 2.

Таким образом, длина гипотенузы равна квадратному корню суммы квадратов катетов:

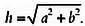
Поскольку отрезок образует треугольник с горизонтальными и вертикальными осями, нам нужно только заменить стороны а и b числами 3 и 4 соответственно, длину стрелки обозначим через l :

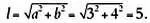
Теперь рассмотрим трехмерное пространство.

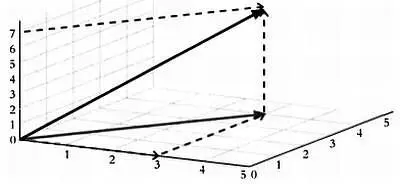
Горизонтальная проекция образует прямоугольный треугольник.

В этом случае длину можно найти в два этапа. Мы видим, что отрезок снова образует треугольник, в котором мы знаем высоту (она равна семи единицам), но не основание. Чтобы найти основание, нужно понять, что оно также является гипотенузой прямоугольного треугольника со сторонами три и четыре, как показано на рисунке. Обозначив основание через h , имеем:

h 2= a 2+ b 2= 3 2+ 4 2= 25.

Используя полученный результат, применим теорему Пифагора к большому треугольнику, высота которого семь единиц, а основание — пять. Обозначим через с высоту, через l длину. Помня, что h 2= a 2 + Ь 2имеем:

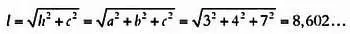
В наших рассуждениях просматривается определенная модель. В двух измерениях длина — это квадратный корень суммы квадратов каждой координаты, то есть:

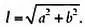
В то время как в трех измерениях длина равна:

* * *

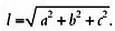
НЕЕВКЛИДОВЫ ПРОСТРАНСТВА

Геометрия, которой мы пользуемся до сегодняшнего дня, была описана греческим математиком Евклидом(ок. 325 до н. э. — ок. 265 до н. э.). В своей книге «Начала» он описал пять аксиом, то есть утверждений, которые Евклид считал истинными, построив на их основе остальную геометрию.

В пятой аксиоме Евклида утверждается, что параллельные прямые никогда не пересекаются. Включение этой аксиомы в число основных вызывало вопросы у математиков: они были убеждены в том, что ее можно вывести из четырех предыдущих. Однако все попытки сделать это не увенчались успехом. В конце концов было решено попробовать другой путь: изменить пятую аксиому и доказать, что это ведет к противоречию. Но, к удивлению математиков, новые геометрии с измененной пятой аксиомой не были противоречивыми. В конце концов ученые вынуждены были признать, что евклидова геометрия не является единственно возможной.

Новые геометрии могут рассматриваться как обобщение понятия расстояния. Вспомним, что длина стрелки вычисляется суммированием квадратов длин сторон и извлечением квадратного корня:

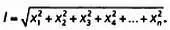
Но мы можем определить расстояние и по-другому. Например, общая теория относительности определяет расстояние в пространстве и во времени. Если с— скорость света, a d— евклидово расстояние, то пространственно-временное расстояние выражается следующим образом:

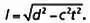
Неевклидовы геометрии больше подошли для описания действительности, чем наш здравый смысл.

* * *

На самом деле, в одном измерении это просто а, которое можно выразить следующим образом:

l = √( a 2)

Рассмотрев эти три выражения, можно сделать вывод, что для получения длины в еще одном измерении нужно прибавить квадрат следующей координаты. Таким образом, в n -мерном пространстве складываются квадраты n координат и извлекается корень суммы. Выражаясь математически, если обозначить n -ную координату через х , то:

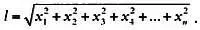
Это выражение легко распространяется на любое число измерений. Таким образом, мы получили формулу для расчета длины стрелки в пространстве с любым количеством измерений. И это потрясающее математическое достижение.

Понятие объема можно определить как количество пространства, которое занимает объект. Можно ли говорить об объемах в других измерениях? Например, подошло бы наше понятие объема обитателям Вселенной из пяти измерений?

Прежде чем анализировать пространства с размерностью больше трех, рассмотрим меньшее количество измерений.

В нашей повседневной действительности объем измеряется в кубических метрах (м 3), кубических сантиметрах (см 3) или в целом в любой единице измерения расстояния, возведенной в куб. Любопытно, что показатель степени единицы измерения объема совпадает с числом измерений пространства, в котором мы живем.

Теперь возьмем другую знакомую величину — площадь. Она измеряется в единицах измерения длины в квадрате, обычно в квадратных метрах, или м 2. Площадь используется для измерения количества пространства, которое занимает плоская, то есть двумерная фигура. Итак, мы можем трактовать площадь как вид объема для двумерных объектов. Точно так же длина соответствует объему одномерных объектов.

Теперь вообразим, что в нашем мире только два измерения. То есть мы существа, ограниченные площадью, как муравьи. В этом мире мы не знали бы понятия объема, а только понятие плоскости. Для нас двумерным эквивалентом объема была бы площадь.

* * *

ФЛАТЛАНДИЯ

«Флатландия» (в переводе с английского "Flatland") — это название романа английского автора Эдвина Эбботта(1838–1926) , в котором для сатирического описания викторианского общества используется понятие пространств из нескольких измерений. Во «Флатландии» рассказывается история о Квадрате, который живет в двумерном мире, где социальный статус каждого многоугольника определяется числом его сторон. Однажды квадрату наносит визит Сфера, которая живет в Трехмерии — трехмерной стране, и рассказывает ему о своей родине. Однако Квадрат отказывается верить в существование третьего измерения, пока не посещает страну своей новой знакомой.