Пере Грима - Том13. Абсолютная точность и другие иллюзии. Секреты статистики

Флоренс Найтингейл умело отбирала данные, отражающие реальность, и проводила грамотный анализ, чтобы понять суть проблемы и возможные способы ее решения. С помощью статистических исследований и грамотно представленных результатов она смогла преодолеть бюрократию и консерватизм военных и убедить верховное командование в необходимости радикального изменения устройства военных госпиталей. Она спасла множество жизней, а многие процедуры, введенные ею, до сих пор применяются в современных больницах. Флоренс Найтингейл — первая женщина, ставшая членом британского Королевского статистического общества.

* * *

Разумеется, вы слышали шутку: если один человек съел целую курицу, а второй остался голодным, то, по статистике, каждый съел половину курицы. Или если вы положите ноги в холодильник, а голову — в духовку, то средняя температура вашего тела будет абсолютно нормальной. Подобные недоразумения возникают из-за того, что мы хотим обобщить информацию исключительно с помощью средних значений, не учитывая разброс данных. Еще один пример, указывающий на эту же ошибку, — это попытка определить благосостояние жителей страны, учитывая только средний доход на душу населения. Если бы у вас была возможность выбрать, в какой стране родиться, то следовало бы обращать внимание не только на средний доход, но и на его разброс (вариацию). Лучше жить в стране, где каждому гарантирована четверть курицы, чем в той, где в среднем каждому достается половина курицы, но велика вероятность остаться ни с чем. В конечном счете чтобы обобщить информацию, содержащуюся в объемной выборке данных, нужно также измерить их вариацию. Для этого используются различные показатели, о которых мы расскажем далее.

Размах вариации

Размах вариации — это разность между наибольшим и наименьшим значением. Например, если дана выборка 2, 6, 7,12,12,18, размах вариации равен 18 — 2 = 16. Этот показатель очень просто вычислить, но он обладает определенным недостатком: в нем не учитывается информация, содержащаяся во всей выборке. Анализ только крайних значений, которые могут встречаться очень редко, явно недостаточен, особенно если выборка велика. Если элементов выборки мало (например, 4–5), размах вариации — подходящий показатель. Если число элементов выборки равно двум, то этот показатель столь же удобен, как и все остальные.

Дисперсия и среднеквадратическое отклонение

Наиболее часто используемый показатель вариации — среднеквадратическое отклонение. Чтобы определить его, начнем с дисперсии, так как среднеквадратическое отклонение рассчитывается как квадратный корень из дисперсии.

Если бы мы хотели разработать какой-то показатель вариации, то очевидно, что в его расчете должны были бы использоваться все данные, как в случае со средним арифметическим. Например, дана выборка 1, 2, 4, 7 и 9. Можно вычислить среднюю разность между каждым значением и средней величиной, равной 4,6:

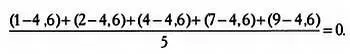
Однако этот показатель всегда будет равен нулю вне зависимости от того, какими будут элементы выборки. Следовательно, он не имеет смысла (его значение одинаково вне зависимости от вариации). Используем абсолютные значения разностей:

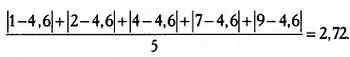
Этот показатель называется среднее абсолютное отклонение. Он достаточно удобен, так как большему разбросу данных соответствует большее значение этого показателя. Но все же гораздо более интересными свойствами обладает показатель, в котором проблема взаимного сокращения разностей решается путем возведения их в квадрат:

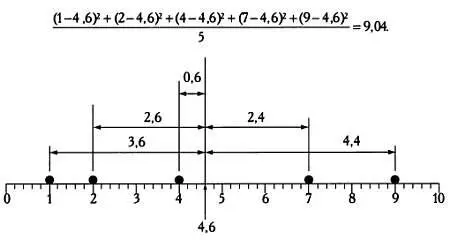
Разность между каждым значением и средним арифметическим 4,6. Дисперсия — среднее значение квадратов этих разностей.

Этот показатель называется дисперсией. Он позволяет оценить разброс значений, а также лежит в основе многих статистических методов. Дисперсия обозначается δ 2. Недостаток дисперсии заключается в том, что ее единица измерения — это единица измерения исходных данных, возведенная в квадрат. Если исходная выборка состоит из значений длины в метрах, единицей измерения дисперсии будет квадратный метр, что несколько усложнит интерпретацию. Решение этой проблемы очень простое: нужно всего лишь извлечь из дисперсии квадратный корень.

Полученное значение, которое мы будем обозначать δ , называется среднеквадратическим отклонением и является самым распространенным показателем вариации. Обобщение большой выборки данных очень часто производится с помощью всего двух показателей: среднеквадратического отклонения и среднего арифметического.

* * *

НЕМНОГО ФОРМУЛ

Общая формула расчета дисперсии такова:

где x i— значения элементов выборки, μ — среднее арифметическое, N — число элементов выборки. Формула расчета среднеквадратического отклонения такова:

* * *

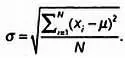
Коэффициент вариации

Какая величина варьируется больше — вес котов или вес коров? Допустим, что средний вес кота равен 4 кг и в 95 % случаев он лежит в интервале от 3 до 5 кг. Предположим, что вес коровы в 95 % случаев лежит в интервале от 480 до 500 кг. Если мы изучим вес котов, то увидим, что он варьируется очень сильно (некоторые коты весят почти в два раза больше других), а вес коров различается несущественно.

Среднеквадратическое отклонение веса котов будет находиться в пределах 0,5 кг. В соответствии с закономерностью вариации весов, 95 % выборки отстоит от среднего значения не более чем на два среднеквадратических отклонения. Об этом будет рассказано в следующей главе, посвященной нормальному распределению. Среднеквадратическое отклонение веса коров будет лежать в пределах 5 кг, что в 10 раз больше, однако вес коров варьируется меньше.

Чтобы разрешить этот парадокс, возникающий при сравнении вариаций, вводится коэффициент вариации, который равен частному среднеквадратического отклонения и среднего значения:

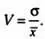
В нашем примере коэффициент вариации для веса котов равен 0,125, для веса коров — 0,01. Коэффициент вариации — безразмерная величина.