Пере Грима - Том13. Абсолютная точность и другие иллюзии. Секреты статистики

Если целью продавца является рост дохода, то она выполнена всего на 50 %. Однако если мы будем считать целевым значением объем продаж в 10,6 миллиона, а фактическим — 10,3, то получается, что цель выполнена на 97,2 %.

Операции с процентами также стоит выполнять очень внимательно.

1. Если цена товара увеличилась на 20 %, а затем снизилась на 20 %, каким будет соотношение начальной и конечной цены? Цена товара изменится: она уменьшится на 4 %. Обозначив исходную цену за х , получим, что итоговая цена равна ( х + 0,2 х ) — 0,2( х + 0,2 х ) = х — 0,04 х .

2. Товар состоит из 10 компонентов. Стоимость каждого компонента возросла на 2 %. На сколько увеличится стоимость товара? Она возрастет на 2 %. Цена отдельных компонентов в этом случае не имеет значения. Если вы все еще сомневаетесь, выполните расчеты вручную и убедитесь в этом самостоятельно.

3. Если Иван зарабатывает на 1000 % больше Петра, он получает в 11 раз больше, а не в 10, как может показаться. Если он зарабатывает на 100 % больше, он получает в два раза больше, если на 200 % больше — то в три раза больше.

В действительности всё не так. Парадокс Симпсона

Когда приводятся проценты для нескольких групп, каждая из которых разбита на подгруппы, может показаться, что налицо определенная зависимость. Однако истинная зависимость будет прямо противоположной. Это явление известно под названием парадокс Симпсона. Рассмотрим пример.

Крупная компания открывает новый завод и создает 250 рабочих мест в службе продаж, монтажа и в складской службе. На рабочие места претендовали 355 мужчин и 325 женщин. Работу получили 190 мужчин (53,5 %) и 60 женщин (18,5 %). Уровень подготовки мужчин и женщин был абсолютно одинаков. Можно ли утверждать, что имеет место дискриминация женщин при приеме на работу? Нет, это не так. Исходные данные таковы:

В действительности процент принятых на работу в каждом отделе выше среди женщин. Причина в том, что в службе, куда было принято больше всего сотрудников, рабочие места получили много мужчин и мало женщин, а в других службах, где требовалось меньше сотрудников, ситуация была обратной.

В начале раздела мы приводили цитату о том, что 65 % молодых людей 10–17 лет пользовались видеоиграми для взрослых. Взята она из реального газетного заголовка. В статье объясняется, откуда взята цифра в 65 %: автор сложил положительные ответы 50 % юношей и 15 % девушек! Любопытно, каков был бы результат, если бы на этот вопрос положительно ответили 50 % юношей и 60 % девушек?

Решим еще одну задачу. Владелец пекарни обеспокоен тем, что, как ему кажется, вес готовых булок различается слишком сильно и некоторые булки могут весить меньше, чем допускается стандартом. Для выпечки используются две печи, в которых выпекают хлеб два оператора. В какие-то дни работает первый оператор, в какие-то — второй. В следующей таблице указан вес (в граммах) для выборки булок. Измерения производились в течение 20 дней:

Вес булки должен равняться (220 ± 10) граммов. Допустим, что представленная выборка является репрезентативной. Нужно ответить на вопросы, действительно ли существует проблема; что происходит; что нужно сделать, чтобы устранить проблему, если она вообще существует.

Если вы попытаетесь сделать какие-то выводы «на глаз» на основании данных, представленных в таблице, то, скорее всего, ошибетесь. Хотя речь идет всего о 160 значениях, выводы, сделанные «на глаз», скорее всего, будут неточными. Также не следует погружаться в объемные вычисления или использовать сложные методы. Достаточно представить данные графически, как показано далее.

Гистограмма веса 160 хлебобулочных изделий.

Эта диаграмма называется гистограммой. Она крайне полезна для анализа вариации данных.

В нашем примере гистограмма указывает, что проблема действительно существует, так как вес некоторых булок меньше минимально допустимого. Иными словами, речь идет не об исключениях, а о естественной вариации веса булок.

На следующих гистограммах представлены данные по каждой печи и по каждому оператору в отдельности. Из них четко видно, что неполадки присутствуют в печи № 2, так как центральное значение на соответствующей диаграмме смещено. С печью № 1 все в порядке, и данные для обоих операторов практически совпадают.

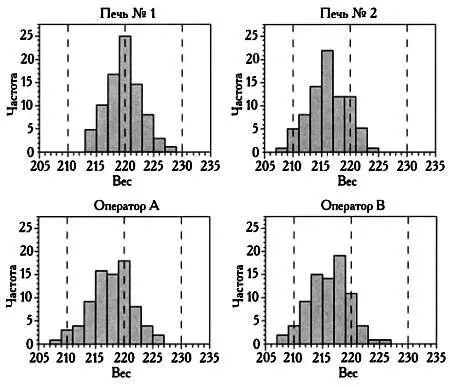
Вес булок для каждой печи и каждого оператора в отдельности.

Даже для очень малого объема данных, например для такого:

21,1; 17,8; 19,7; 18,6; 16,8; 21,7; 28,7; 20,1; 19,5; 17,8,

на простой точечной диаграмме видны подробности, которые можно упустить при простом анализе данных «на глаз». В этом случае видно, что одно значение существенно отличается от остальных, и следует проанализировать причины подобного отклонения (возможно, это простая опечатка: оператор ввел 28,7 вместо 18,7). Эти вопросы крайне важны, так как ошибка в исходных данных может перечеркнуть всю проделанную работу.

Представление множества данных с помощью точечной диаграммы.

Если мы хотим учесть порядок выборки данных, гистограммы и точечные диаграммы нам не помогут. Для этого нужно представить данные в виде временного ряда, как показано на следующем рисунке, где четко заметно увеличение среднего роста населения Испании на протяжении XX века. Разумеется, на основе графиков подобного типа нельзя делать экстраполяции: вовсе не факт, что через 1000 лет средний рост будет находиться у отметки 2 м 70 см.

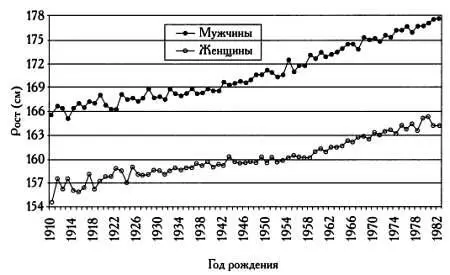
Изменение среднего роста населения Испании в период с 1910 по 1982 год.

(Источник: X. Спийкер, X. Переси А. Камара. Изменение среднего роста населения Испании в XX веке по результатам исследования министерства здравоохранения. Журнал Estadistica Espahola, № 169, 2008 г.)

Помимо стандартных графиков, которые мы только что рассмотрели, круговых и им подобных диаграмм, можно использовать и другие, не столь известные. Существует, например, диаграмма «стебель — листья».

Рассмотрим практический пример. Группу из 92 студентов попросили измерить пульс. На гистограмме на следующей странице представлены полученные значения (все данные, использованные в этом примере, содержатся в файлах примеров пакета статистических программ Minitab ).

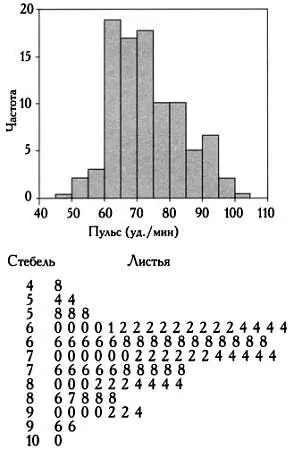
Гистограмма и диаграмма «стебель — листья», на которых представлены данные о пульсе для группы из 92 студентов.