Хавьер Арбонес - Том 12. Числа-основа гармонии. Музыка и математика

Берлину удалось достичь этого удивительного эффекта за счет «сжатия» нот. На следующей иллюстрации можно видеть, как четыре ноты, сгруппированные в фигуры и обозначенные кругами под номерами от 1 до 4, следуют друг за другом. Стрелкой обозначена граница такта.

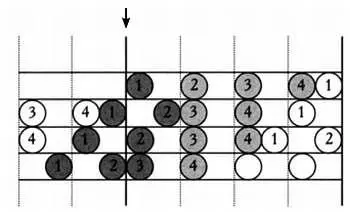
Вертикальное масштабирование

Что происходит при вертикальном масштабировании? Это преобразование — самое необычное из рассмотренных нами. Его сложнее всего выполнить и весьма непросто услышать в музыкальной композиции. При вертикальном масштабировании все интервалы пропорционально расширяются. В первом примере интервалами мелодии являются две терции. Во втором примере терции преобразуются в квинты.

Подобное повторение расширенной мелодической кривой исходной мелодии иногда может давать пародийный эффект. Известный пример вертикального мас штабирования связывает между собой Баха и Джона Кейджа и упоминается в классической научно-популярной книге «Гедель, Эшер, Бах» американского автора Дугласа Хофштадтера(р. 1945) .

Если использовать латинскую систему, в которой ноты обозначаются буквами от А до G , то с помощью масштабирования можно превратить тему ВАСН («Бах») в CAGE («Кейдж»).

Интервалы темы BACH : —1|+3 |—1.

Умножив эти интервалы на 3, получим —3 |+9 |—3, что почти совпадает с темой CAGE , интервалы которой равны —3 |+10 |—3.

Симметричные аккорды

Одна октава состоит из 12 полутонов. Эти 12 полутонов можно разделить на симметричные аккорды всего двумя способами: в первом случае аккорды из 3 нот будут разделены 4 полутонами, во втором случае аккорды из 4 нот будут разделены 3 полутонами.

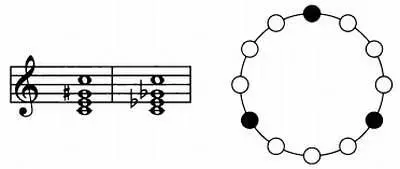
В первом случае образуется аккорд увеличенной квинты, состоящей из двух больших терций, во втором — аккорд уменьшенной септимы. Благодаря своей симметричности этот аккорд занял очень важное место в истории музыки, так как его можно «прочитать» многими способами одновременно.

Симметричные звукоряды

В своей книге «Техника моего музыкального языка» французский композитор Оливье Мессиан(1908–1992) приводит классификацию звукорядов, которые он называет ладами ограниченной транспозиции. В этих звукорядах, ступени которых образуют полную октаву, интервалы, разделяющие ноты, распределяются симметрично. Такие звукоряды основаны на хроматической системе из 12 звуков и состоят из различных симметричных групп. После определения звукоряда он последовательно транспонируется до тех пор, пока при транспозиции не образуется звукоряд, в котором будут полностью повторяться ноты исходной группы.

Первый лад в классификации Мессиана называется ладом с целыми тонами:

В этом ладу допускается всего два варианта: первый начинается с до , второй — с до-диез . В ладу, который начинается с ре , повторяются ноты исходного лада.

Второй лад — уменьшенный октатонический звукоряд, в котором чередуются полутона и целые тона. Этот лад делится на четыре группы по три ноты и допускает три транспозиции.

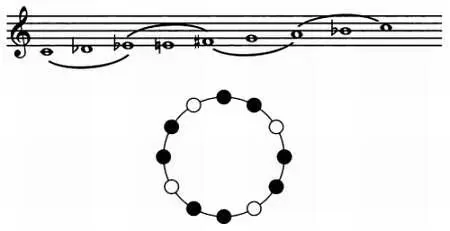
Третий лад образован последовательностями тон — полутон — полутон, состоит из трех групп по четыре звука и допускает четыре транспозиции.

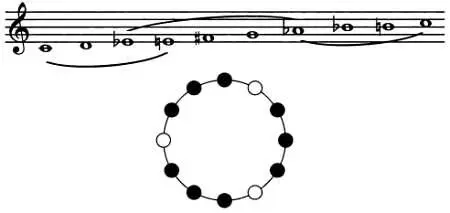
Порядок интервалов в четвертом ладу таков: полутон — полутон — полтора тона (3 полутона) — полутон, шесть транспозиций.

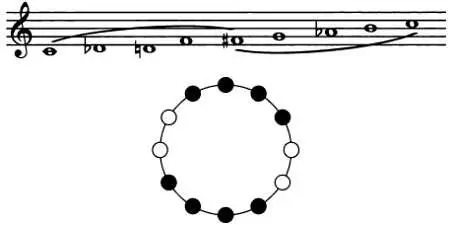
Пятый лад образует две симметричные группы из четырех звуков: полутон — два тона — полутон и допускает шесть транспозиций.

Шестой лад состоит из двух групп по шесть звуков (тон — тон — полутон — полутон) и допускает шесть транспозиций.

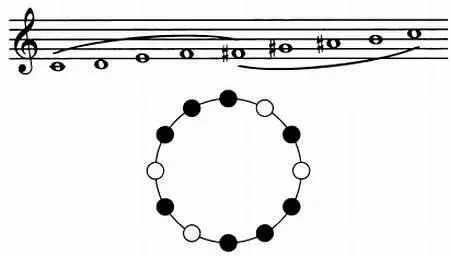
Седьмой лад состоит из двух групп по шесть звуков (полутон — полутон — полутон — тон — полутон) и допускает шесть транспозиций.

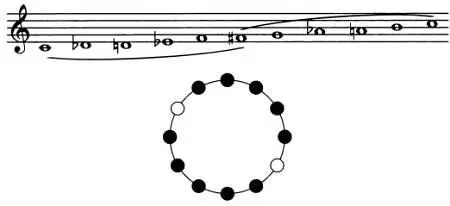
Симметрия наблюдается не только в музыкальных фразах и мотивах. Более сложные музыкальные структуры также могут обладать интересными математическими свойствами.

В формальном анализе музыкальных произведений изучается «музыкальная плоскость» — иными словами, составные части произведения и взаимосвязи между ними. Так как «музыкальную плоскость» можно изображать с разной степенью точности, в зависимости от «масштаба» можно получить общее представление, не содержащее нюансов, либо, напротив, в подробностях увидеть все детали, но не все произведение в целом.

ABCDE…

Рассмотрим музыкальные произведения издалека. Мы увидим крупные структуры, которые будем обозначать заглавными латинскими буквами. Здесь в качестве структурных элементов композиции мы будем рассматривать повторяющиеся или изменяющиеся фрагменты произведения. Композицию, в которой полностью повторяется единственная группа, будем обозначать так:

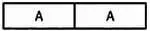
Такие композиции обладают простой симметрией. Произведение, состоящее из двух полностью различных групп, напротив, не обладает какой-либо симметрией:

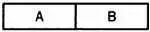
Существуют ли произведения, симметричные с формальной точки зрения? Да, такие произведения существуют, более того, они встречаются очень часто. Примером может служить скерцо («игра») — произведение, которое обычно является частью другого, более крупного произведения, например симфонии. В качестве примера можно привести скерцо из Девятой симфонии Бетховена или скерцо из Симфонии № 4 Чайковского. По своей сути скерцо имеет вид АВ . Иногда после исполнения второй части первая повторяется заново, и композиция принимает вид: