Хавьер Арбонес - Том 12. Числа-основа гармонии. Музыка и математика

Согласно второму подходу, интервалы можно также представлять в численном виде как соотношение частот нот. В этом случае имеет значение не абсолютная частота звука каждой ноты, а отношение между их частотами. Тогда две ноты можно сравнить, указав разделяющий их интервал в виде отношения частот соответствующих звуков. Если, например, мы сыграем две ноты, разделенные интервалом в одну кварту, то более высокая нота будет иметь частоту, равную 4/3 частоты более низкой ноты. Если два звука разделены интервалом в одну квинту, то их частоты относятся как 3:2. Например, для ноты ля частотой 440 Гц следующая нота ми , отделенная интервалом в одну квинту, будет иметь частоту в 660 Гц.

* * *

ЛИНЕЙНЫЙ И ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ

Интервал между двумя нотами называется по числу нот, их разделяющих, включая границы интервала. Из-за этого операция сложения интервалов не является интуитивно понятной. Чему равна сумма секунды и терции? Квинте? Достаточно выполнить несложные расчеты, чтобы показать, что это не так. Пусть началом интервала, равного искомой сумме, будет нота до. Прибавив секунду, мы получим ноту ре. Прибавив терцию, получим фа. Таким образом, сумма этих интервалов равна не квинте, а кварте.

Сумма интервалов подчиняется линейному закону. Если мы пронумеруем клавиши пианино, обозначив за 1 самую низкую ноту, за 88 — самую высокую, то увидим, что клавиши, соответствующие ноте ля, имеют номера 1, 8, 15, 22, 29 и так далее. Иными словами, чтобы перейти от одной ноты ляк следующей, нужно перейти на семь клавиш вправо или влево. Однако если мы рассмотрим не клавиши пианино, а частоты соответствующих звуков, то увидим, что они возрастают не линейно, а экспоненциально. Так, самый низкий звук пианино, соответствующий ноте ля, настраивается на частоту 27,5 Гц. Чтобы перейти к следующему ля, нужно не прибавить к этой частоте какое-то фиксированное число, а умножить эту частоту на 2. Таким образом, следующая лянастраивается на 55 Гц, следующая — на 110 Гц и так далее.

* * *

Отношение между длинами двух струн обратно отношению между частотами звуков, издаваемых этими струнами. Например, если звуки разделены квинтой, то есть их частоты относятся как 3:2, то длины этих струн относятся друг к другу как 2:3. Далее мы не будем упоминать о длинах струн, а будем говорить только о частотах звуков.

Так, две ноты, частоты которых равны 440 Гц и 880 Гц, разделены интервалом в одну октаву и настроены в точном соответствии со стандартом для ноты ля . Ноты, частоты которых равны 442 Гц и 884 Гц, также разделены интервалом в одну октаву, хотя настроены не по стандарту. И наконец, ноты, частоты которых равны 443 Гц и 887 Гц, не разделены интервалом в одну октаву. На слух они распознаются как «ненастроенная октава».

* * *

ПРОКЛЯТИЕ АБСОЛЮТНОГО СЛУХА

Абсолютный слух — это способность, позволяющая на слух определять ноты. Если мы нажмем любую клавишу пианино, человек с абсолютным слухом сможет назвать прозвучавшую ноту. Абсолютный слух и музыкальное дарование не связаны между собой. На самом деле многие музыканты страдают от своего абсолютного слуха. Например, в хоровой музыке партитуры часто транспонируют, подстраивая их под тон, в котором будет лучше звучать хор. Песня может исполняться в полном соответствии с партитурой, но на полутон ниже. Исполняемые ноты не совпадут с нотной записью, и музыкант с абсолютным слухом придет в замешательство.

* * *

Соотношение между частотами нот позволяет на основе одного известного звука найти другой, отделенный от исходного любым интервалом. Для этого нужно умножить частоту исходного звука на соответствующий коэффициент. К примеру, зная частоту F 1 можно найти частоту F 2 звука на одну кварту выше, то есть в 4/3 раза больше, следующим образом:

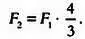
Эту формулу можно последовательно применять несколько раз, используя необходимые множители. Например, если F 3 на одну большую терцию больше (отношение частот звуков будет равняться 5/4), чем F 2 можно вычислить отношение между F 3 и F 1 следующим образом:

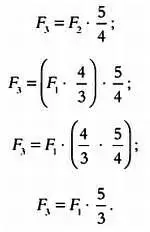
Эти расчеты можно производить и в обратном порядке, используя деление вместо умножения. Например, частота F 4 , которая на одну квинту ниже F 1, вычисляется так:

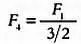
Музыкальная и численная формы представления интервалов тесно связаны между собой. Далее мы будем использовать и ту, и другую форму в зависимости от контекста.

Настройка пианино

Попробуем определить частоты 12 нот одной октавы пианино.

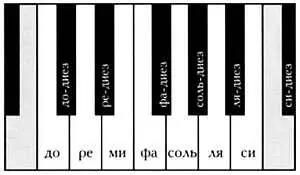
Будем действовать следующим образом: определив частоту одной ноты ре , зададим частоты всех остальных ре путем умножения или деления этой частоты на 2. Выполним аналогичные действия для всех остальных нот.

Нота до будет иметь нормализованное начальное значение, равное 1. Всем остальным нотам будут соответствовать числа в интервале от 1 (начальное до ) до 2 (следующее до ). Эти числа будут соответствовать отношению частоты заданной ноты и начального до . Чтобы настроить пианино, нужно определить эти значения для всех нот. В качестве начального значения для расчетов можно выбрать любое число (например, 440 Гцдля ноты ля ).

12 нот означают, что начальное и следующее до разделяют 12 «шагов». Каждый из этих шагов называется полутоном. Сначала попробуем решить эту задачу, используя результаты, применяемые пифагорейцами при настройке инструментов той эпохи.

Пифагорейский строй

Пифагорейский строй основывался на простых отношениях между различными звуками. В его основе лежали два интервала: октава, соответствующая отношению между частотами звуков 2:1, и квинта, соответствующая отношению 3:2. Пифагорейцы получали различные звуки с помощью последовательности квинт, затем использовали перенос на одну или несколько октав, чтобы найти частоты звуков в необходимом диапазоне.

В качестве примера начнем с ноты до . Сначала найдем частоту звука, отделенного от этой ноты восходящей квинтой, и получим ноту соль . Повторив эти же действия, получим ре , затем ля , затем ми и, наконец, си . Выполнив смещение на одну нисходящую квинту с начального до , получим ноту фа . Так получаются семь звуков пифагорейского строя: