Хавьер Арбонес - Том 12. Числа-основа гармонии. Музыка и математика

фа <���— до —> соль —> ре —> ля —> ми —> си .

* * *

НАЗВАНИЯ НОТ

Греки дали названия нотам по первым буквам ионийского алфавита. Один и тот же звук, измененный на половину тона или сдвинутый на одну октаву, обозначался разными буквами. Например, нота фа обозначалась буквой альфа, бета обозначала фа-диез, гамма — фа-дубль-диез. Звуки пифагорейского строя располагались в порядке убывания, в современном музыкальном строе они расположены с точностью до наоборот.

Римляне также использовали буквы алфавита для обозначения звуков. Боэций, который в V веке н. э. создал пятитомный труд по теории музыки, рассматривал строй из пятнадцати нот, охватывавших две октавы. Каждую из этих нот Боэций обозначил своей буквой, не учитывая цикличность октав. На следующем этапе, разумеется, эта цикличность стала учитываться в названиях нот, и одни и те же ноты разных октав стали обозначаться одинаковыми буквами.

В так называемой английской (или немецкой) нотации семь нот обозначались заглавными латинскими буквами от Адо G, ноты следующей октавы — строчными буквами от а до g,ноты третьей октавы — удвоенными строчными буквами ( аа, bb, сс, dd, ее, ff, gg). Так свои названия получили семь звуков, соответствующие белым клавишам фортепиано. Остальные пять звуков, соответствующие черным клавишам, получили производные от основных звуков названия позднее, с появлением понятий «бемоль», «бекар» и «диез».

В XI веке тосканский монах Гвидо д'Ареццо(ок. 995 — ок. 1050) разработал набор мнемонических правил для чтения нот. Возможно, самым известным из них является так называемая гвидонова рука. В этом методе ноты условно располагаются в алфавитном порядке на пальцах руки. Гвидо д'Ареццо также дал названия всем нотам. Он обозначил каждый звук первым слогом в каждой строке очень известной в то время молитвы Иоанну Крестителю:

Utqueant laxis,

resonare fibris,

Mlra gestorum,

famuli tuorum,

Solve polluti,

Labii reatum,

Sancte lohannes.

Позднее слог ut заменился на do. Так появились названия нот, которые используются и сейчас.

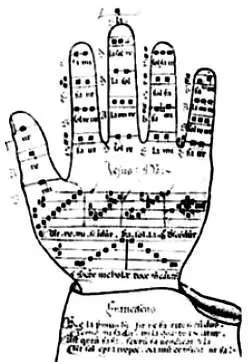
Рисунок «гвидоновой руки» из средневековой рукописи.

* * *

Если продолжить цепочку квинт, получится 12 звуков так называемого хроматического строя, составляющие квинтовый круг:

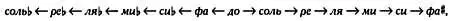
где знаки бемоль ( 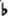) и диез ( #) означают изменение на полутон ниже и выше соответственно.

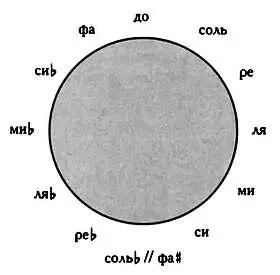
После того как мы получили 12 нот, упорядочив квинты, нетрудно вычислить частоты всех нот, лежащих в пределах одной октавы, путем сдвига на одну или несколько октав.

Подсчеты

Определим частоту каждой ноты с помощью цепочки квинт и сдвига на одну или несколько октав, то есть путем деления и умножения частоты на 2. Напомним, что отношение между частотами звуков всегда будет принимать значение между 1 (соотношение частоты одного и того же звука) и 2 (отношение частот нот до соседних октав).

Сначала определим относительную частоту ноты соль, которая отстоит на одну квинту от ноты до :

соль = 3/2

Затем определим частоту ноты ре , которая отстоит на одну квинту от соль (необходимо умножить частоту на 3/2), но потребуется сдвиг на одну октаву ниже (умножить частоту на 1/2):

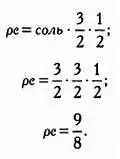
Расстояние между до и ре называется целым тоном. Как и следовало ожидать, один тон равен двум полутонам.

Затем определим относительную частоту ноты ля , отстоящей на одну квинту от ре :

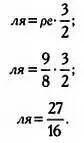
Нота ми отстоит на одну квинту от ля , но потребуется сдвиг на одну октаву ниже:

Последние ноты строя — си , отстоящая на одну квинту от ми , и фа , для получения которой необходим сдвиг на одну квинту ниже до с последующим смещением на одну октаву выше (потребуется умножить частоту на 2).

Приняв частоту до за 1, представим частоты всех нот в таблице:

Можно повторить эти же действия, чтобы определить частоты бемолей, соответствующих черным клавишам пианино.

Для этого нужно последовательно выполнять сдвиг на одну квинту ниже, начиная с ноты фа .

Пифагорейская комма

На одну квинту выше ноты си находится фа-диез , который должен совпадать с соль-бемоль . Но это не один и тот же звук: разница между фа-диез и соль-бемоль называется пифагорейской коммой. Аналогично, определив частоты фа-диез и ре-бемоль , мы увидим, что они отстоят друг от друга не на одну кварту, а на интервал, который отличается от квинты на одну пифагорейскую комму. Эта квинта, которая немного меньше настоящей, называется волчьей квинтой.

Построив квинтовый круг из 12 квинт, мы получим ноту, которая немного отличается от первоначальной и отстоит от нее на семь октав:

Это «немного» и есть пифагорейская комма. Ее значение (обозначим его ПК) можно вычислить, взяв за основу частоту f и сравнив цепочку из 12 квинт, начиная с f , с цепочкой из семи октав:

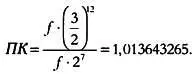
Отличие будет чуть больше 1 % октавы или, что равносильно, почти четверть полутона. Это отличие вызвано тем, что дробь, соответствующая квинте, несовместима с дробью, соответствующей октаве, что нетрудно показать. Для этого попробуем найти такие показатели степеней х и у , которые позволят связать эти две дроби: