Хавьер Арбонес - Том 12. Числа-основа гармонии. Музыка и математика

— круг с точкой в центре обозначал трехдольный такт с трехдольным ритмическим делением, что эквивалентно современному размеру 9/8;

— круг без точки в центре обозначал трехдольный такт с двухдольным ритмическим делением, что эквивалентно современному размеру 3/4;

— полукруг с точкой внутри обозначал двухдольный такт с трехдольным ритмическим делением, что эквивалентно современному размеру 6/8;

— полукруг без точки обозначал двухдольный такт с двухдольным ритмическим делением, что эквивалентно современному размеру 2/4.

В следующей таблице описываются эти четыре разновидности ритма, приведены обозначения той эпохи и соотношения между различными фигурами. Для темпус перфектум и большой пролации бревис (обозначен квадратом) равен трем семибревисам (ромбам), каждый из которых равен трем минимам (обозначены ромбом с вертикальной чертой):

* * *

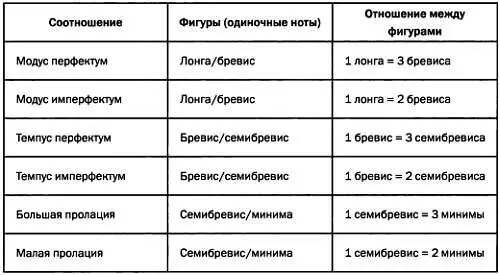
ЯВЛЕНИЯ И ИХ ПРЕДСТАВЛЕНИЯ

Подобно тому как математические модели являются отображением реальности, так и музыкальная нотация является графическим представлением физического явления, но не наоборот. Партитура незнакомого произведения дает музыканту лишь приближенное представление о том, что хотел выразить композитор. Достаточно послушать одно и то же произведение в исполнении различных музыкантов, чтобы оценить различия. Нечто подобное происходит, когда мы читаем написанный текст или слышим, как его произносит кто-то другой: когда актер декламирует стихотворение, он наделяет слова необъяснимой экспрессией, и эту магию актерской игры нельзя передать на бумаге. Карта страны — лишь двумерное графическое представление территории. Карта — это не страна, но карта содержит указания, которые помогут путешественнику найти дорогу. Партитура передает технические аспекты исполнения музыки, но ее интерпретация зависит от музыканта. Именно музыкант завершает произведение и наделяет его смыслом.

* * *

Ударные: чистый ритм

На ритм «накладываются» мелодия, лиги, изменения высоты и интенсивности звуков. При игре на ударных, напротив, ритм остается «обнаженным». Он содержит резкие скачки громкости, высоты и тембра звуков, однако при игре на ударных, по сути, возможны только два варианта: удар или его отсутствие. Здесь ритм проявляется во всей безупречности, раскрывает всю свою сущность. Ритм идеально подходит для изучения с точки зрения математики.

При игре на ударных инструментах циклические последовательности звуков характеризуются распределением артикуляций. Будем записывать исключительно артикуляции без учета эха, удлиняющего звуки. Так мы сможем зафиксировать четкую артикуляцию и понять последовательность звуков.

Можно выделить три различных ощущения ритма в зависимости от его быстроты:

— первый уровень, самая быстрая артикуляция, соответствующая ритмическому делению долей. Удары нумеруются начиная с первой доли по порядку: 1, 2, 3 и так далее. Когда начинается новая доля, отсчет возобновляется с единицы;

— второй уровень образуют относительно сильные доли, которые обозначаются цифрой 1;

— на третьем уровне появляются акценты — доли, которые звучат сильнее других.

Ритмическая последовательность размером 9/8 на трех описанных уровнях будет выглядеть так:

Рассмотрим подробнее вторую строку таблицы, где записаны только доли. Заполнив пустые ячейки таблицы нулями, мы получим четкое представление о последовательности долей. Каждая единица означает удар, ноль — паузу. В результате мы получаем чистый ритм.

Доли образуют структуру, лежащую в основе всей музыки подобно тому, как ткань формируется переплетением тонких нитей с нитями основы. Выберем в качестве единицы измерения ударов восьмую ноту, которую укажем как . Так как ритм образован последовательностью ударов и пауз, будем использовать только восьмые ноты и восьмые паузы. Восьмые паузы обозначим 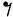. Назовем четвертной нотой последовательность из удара и паузы (из восьмой ноты и восьмой паузы). Отметим ее 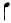. И наконец, добавим в нашу нотацию еще один новый символ, так называемую четвертную ноту с точкой, 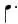— для обозначения тех случаев, когда за одной паузой следует другая, то есть последовательность нот и пауз выглядит как .

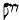По сути, мы рассматриваем двоичную систему, где нотам и паузам присваиваются значения 1 и 0 соответственно. Эквиваленты этих символов для такта размером 4/4 записываются так:

Заметим, что последовательность удар-пауза-удар-пауза повторяется дважды. Двухдольный такт, каждая из долей которого длится одну четвертную ноту с точкой (6/8), будем обозначать так:

Покрытие пространства звуков

В следующей главе мы более подробно проанализируем структуру канонов, а пока ограничимся их ритмическим аспектом, который называется ритмическим каноном.

Одновременное исполнение различных ритмических единиц — серьезная задача для исполнителя, как для солиста, так и для группы. Чтобы познакомиться с тем, что такое ритмический канон, рассмотрим упражнение.

Начнем с ритма 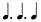= 3 + 3 + 2= 10010010, который циклически исполняют два музыканта. Второй музыкант начинает играть после первой артикуляции первого исполнителя:

Можно увидеть, что в столбцах таблицы под номерами 3, 6, 11 и так далее (выделены жирным шрифтом) паузы обоих ритмов совпадают. Существуют ритмические рисунки, которые можно исполнить в каноне так, что будут выполняться следующие условия:

1) два музыканта не начинают играть одновременно;

2) паузы ритмических рисунков никогда не накладываются друг на друга.

Эту ситуацию можно сравнить с математической задачей замощения плоскости, в которой требуется покрыть всю плоскость правильными геометрическими фигурами. Однако в нашем случае мы хотим покрыть всю «звуковую плоскость».