Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

* * *

СОСТАВЛЕНИЕ РАСПИСАНИЯ С ИСПОЛЬЗОВАНИЕМ КРИТИЧЕСКИХ ПУТЕЙ

В отраслях, где в производственной цепочке задействуется различное оборудование и персонал, интерес представляют алгоритмы производства, методы составления расписания и анализ критических путей. Наиболее важным для этого является изучение зависимостей между задачами или их отсутствия. Рональд Грэхем разработал алгоритм обработки списка задач с помощью mобработчиков. При оптимальном времени выполнения задач Т алгоритм гарантирует, что будет найдена последовательность, время выполнения которой не будет превышать (2 — (1/ m)) Т. Обработчиком может быть человек, устройство или система, время работы которых запрограммировано. В алгоритме, в котором задачи выполняются в порядке убывания сроков выполнения, общее время не будет превосходить [4/3 — 1/(3 m)] Т. Однако никогда не стоит недооценивать частные эвристические решения.

* * *

Система PERT, которую мы сейчас обсудим, основана на следующих принципах.

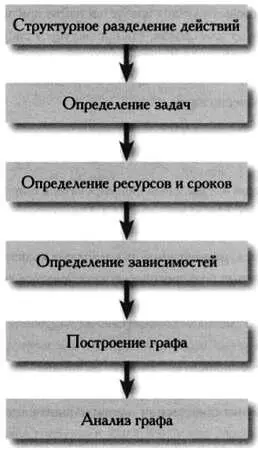
1. Формируется упорядоченное структурное разделение задач проекта. Разделение задач может выполняться с помощью органиграммы, на которой отображаются основные действия. Также можно сформировать группы действий, которые должна выполнить каждая группа, участвующая в реализации проекта.

2. Определяются задачи. Описание основных задач и необходимых технологий позволяет разграничить участки проекта. На этом этапе определяются все действия и их последовательность.

3. Каждой задаче присваиваются ресурсы, фиксируются сроки выполнения задач. Здесь необходимо составить «календарь» реализации проекта, в котором будет указано общее время и время выполнения отдельных действий с учетом всех возможных факторов: ресурсов, технологий, рабочих групп и так далее.

Одна из оригинальных особенностей PERT — введение различных понятий времени:

а) Т о — оптимистичное время выполнения, достигающееся при безукоризненном выполнении всех задач без сбоев;

б) Т р — пессимистичное время, в котором учитываются все возможные действия и события, препятствующие выполнению проекта;

в) Т т — среднее, или вероятное время, или время, рассчитанное с помощью статистических методов на основе прошлого опыта;

г) Т е — реальное время, которое используется в PERT для каждого действия и рассчитывается по формуле (обосновывается статистически):

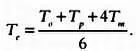
Иными словами, реальное время вычисляется как средневзвешенное оптимистичного, пессимистичного и среднего времени. Также рассчитывается стандартная ошибка ( Т p + Т o )/6, квадрат которой будет оценкой отклонения.

4. Анализируются и определяются зависимости. На этом этапе определяются все возможные зависимости между действиями проекта: ограниченность ресурсов, физического пространства, рабочих групп; ограничения, вызванные особенностями месторасположения, и другие.

5. Формируется сеть, или граф, который является основной моделью системы.

При построении этого графа нужно руководствоваться следующими правилами:

а) события (начало или завершение действия) являются вершинами графа. Они изображаются кругами и прямоугольниками, внутри которых записывается название события и его порядковый номер;

б) действиям соответствуют ребра, или дуги графа, которые соединяют соответствующие события. Над каждым ребром указывается число, обозначающее реальное время выполнения этого действия ( Т е ).

Также существуют дополнительные правила, которые способствуют эффективному построению графа и облегчают его прочтение:

а) каждое действие имеет одно предыдущее и одно последующее событие.

Можно вводить фиктивные действия нулевой длительности, что равносильно записи одного и того же события несколько раз под разными номерами, если это действие имеет несколько последующих;

б) событие считается произошедшим только тогда, когда выполнены все предшествующие ему действия;

* * *

ПРИМЕР ИСПОЛЬЗОВАНИЯ СИСТЕМЫ PERT В СТРОИТЕЛЬСТВЕ

Далее приведен пример анализа строительства дома (точнее, начальных действий) по системе PERT. Нужно составить список начальных задач, присвоить каждой задаче букву или номер, а также определить зависимости и примерное время выполнения ( Т e) каждой задачи.

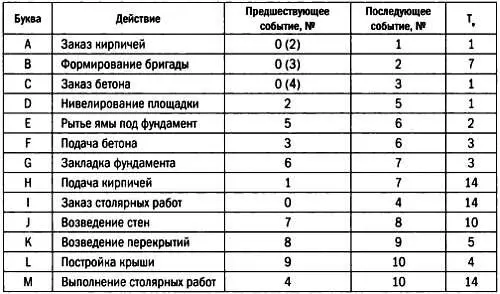
Теперь можно построить соответствующий граф, расположив рядом с каждой его вершиной квадрат и треугольник. В квадратах будем указывать день от начала работ, когда может начаться событие, в треугольниках — день его завершения.

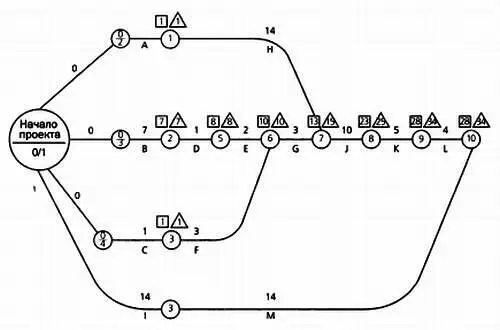
Продолжение графа (вплоть до завершения работ) приведено на следующем рисунке.

* * *

в) следует избегать ситуаций, когда предшествующее и последующее событие для двух действий совпадают. Этого можно избежать путем ввода фиктивных событий нулевой длительности;

г) необходимо создать промежуточные события и фиктивные действия, чтобы устранить вершины 4-й степени и выше;

д) никакое событие не может быть одновременно начальным и конечным в последовательности событий.

6. Наконец, анализируется построенный граф. Например, интерес представляют следующие параметры:

а) дата, наиболее удаленная от завершения проекта, то есть дата начала первого события в последовательности событий;

б) допустимый крайний срок. Завершение события позднее этого срока негативно повлияет на проект в целом;

в) продолжительность события — разница между двумя предыдущими параметрами;

г) избыток времени, доступный при реализации данного действия;

д) критический путь — путь на графе с наибольшим временем выполнения (между двумя данными событиями или для всего графа).

Так называемая система PERT/COST имеет ту же структуру, но в ней учитываются не сроки выполнения задач, а их стоимость. Система PERT также допускает комбинирование сроков и финансовых затрат. В настоящее время для всех систем планирования разработаны простые в использовании информационные системы.

Многие свойства фигур, которые изучаются в геометрии, зависят от их параметров: величин углов, расстояний, перпендикулярности прямых, площади фигур, объема тел и так далее. Однако теория графов и топология помогли выявить геометрические закономерности, которые не зависят ни от параметров геометрических фигур, ни от их формы. В этой короткой главе мы расскажем об известной формуле Эйлера и обнаружим множество ее удивительных следствий, которые проявляются в многогранниках и мозаиках.