Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

* * *

ТОЧНЫЙ ПОДСЧЕТ

Пусть Р— выпуклый многогранник с r( Р ) гранями. Рассмотрим два его параметра:

r( Р ) — количество натуральных чисел i, таких что в Рсуществует грань с iребрами;

К( Р ) — число сторон грани Р с наибольшим числом вершин или ребер.

Так, в кубе Р r( Р ) = 1, К( Р ) = 4. Для пирамиды Р, в основании которой лежит пятиугольник, r( Р ) = 2, К( Р ) = 5.

Если многоугольник Римеет грань, число сторон которой равно К( Р ), так как каждая из этих сторон является ребром другой грани, то общее число граней будет равно как минимум К( Р ) + 1, то есть

С( Р ) >= К( Р ) + 1.

Так как r( Р ) не может быть больше, чем число элементов множества {3, 4, 5, К( Р )}, то

r( Р ) = < К( Р ) — 2.

На основании вышеприведенных неравенств для С( Р ) и r( Р ) имеем:

С( Р ) — r( Р ) >= К( Р ) + 1 — ( К(Р) — 2) = 3.

Если бы все грани многогранника были бы различны, то выполнялось бы равенство С( Р ) = r( Р ) + 3, что невозможно.

* * *

Если вы не привыкли следовать правилам, то возможно, что вы задавались вопросом, существуют ли фигуры без повторяющихся элементов. Например, существует ли многогранник, все стороны которого являются различными многоугольниками: один треугольник, один четырехугольник, один пятиугольник и так далее. Это был бы образцовый многогранник — он мог бы поворачиваться разными сторонами и демонстрировать разные многоугольники. Живительно, но подобный многоугольник не может существовать. И этому есть очень красивое доказательство, в котором используются методы комбинаторики.

Представим на мгновение все возможные многогранники — правильные или неправильные. Если мы нарисуем все эти многогранники, то заметим, что всегда существует как минимум несколько граней, которые являются выпуклыми многоугольниками с одинаковым числом сторон. Чтобы ограничить многоугольниками какую-то область пространства, необходимо чтобы как минимум несколько из них повторялись.

Графы и мозаики

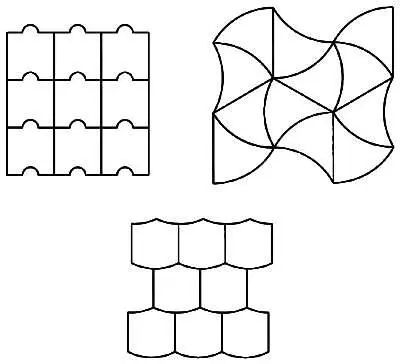
Рассмотрим три разных мозаики, которые представлены на рисунке. Все они, несомненно, знакомы вам, так как часто встречаются в повседневной жизни.

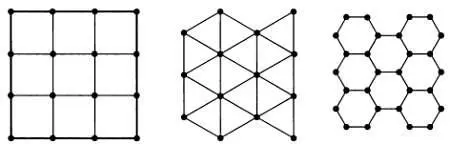
Это четырехугольная, треугольная и шестиугольная мозаики соответственно. Каждая из них представляет собой геометрический граф (определение геометрического графа приводилось выше). Число граней в этих графах может увеличиваться бесконечно: любым из этих графов можно заполнить всю плоскость. Заметим, что при увеличении мозаики для вершин, находящихся внутри, число ребер остается неизменным, и каждая грань ограничивается одним и тем же числом ребер за исключением бесконечно удаленных граней. Если на каждом шаге увеличения мозаики мы будем подсчитывать число вершин V и число вершин V c , расположенных на краю (во внешнем цикле графа), то увидим, что с ростом V отношение V c / V стремится к нулю.

Это справедливо для всех трех рассмотренных типов мозаики. Далее мы продемонстрируем удивительный результат, основанный на следующем определении.

Правильная мозаика — это геометрический граф, который может покрыть плоскость; при этом число ребер а , сходящихся в каждой вершине, и число ребер Ь >= 3 каждой грани являются постоянными (за исключением внешних граней), причем V c / V стремится к нулю.

Единственно возможными правильными мозаиками в соответствии с этим определением являются треугольная, четырехугольная и шестиугольная мозаики.

Пусть дана правильная мозаика М , которая имеет V вершин, А ребер и V c граничных вершин. Тогда 2 А < aV , так как aV — это общее число ребер, получаемое, если поставить в соответствие каждой вершине (включая граничные) а ребер.

Если же мы не будем учитывать ребра, которые выходят из граничных вершин, получим аV — aV c < 2 А .

Объединив эти два неравенства, имеем aV — aV c < 2 А < a V .

Разделим все части неравенства на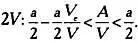

Перейдем к пределу. При V , стремящемся к бесконечности, V c / V стремится к нулю:

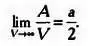
Подсчитаем число граней С мозаики М . С — 1 грань будет иметь Ь ребер, бесконечно удаленная грань будет иметь V c ребер. Следовательно,

( C — 1) b + V c = 2 А .

Разделив на bV , получим:

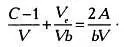
Перейдя к пределу при V , стремящемся к бесконечности, с учетом выражения (*) получим:

(**)

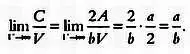
Так как мозаика М — это геометрический граф, для нее выполняется формула Эйлера, которую можно записать в следующем виде:

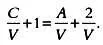
При переходе к пределу имеем:

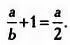
Иными словами, постоянные а и Ь связывает равенство

2 а + 2 Ь = ab ,

что можно записать в таком виде:

( а — 2)( Ь — 2) = 4.

Все возможные натуральные решения этого уравнения представлены в таблице:

Интересно, что это доказательство относится исключительно к теории графов и не зависит от каких-либо геометрических свойств (расстояний, углов, параллельности сторон) фигур, образующих мозаику. Например, следующие мозаики относятся к тем же трем типам, хотя очевидно состоят из других фигур. Единственная разница заключается в изоморфизме соответствующих им графов.

* * *

ФОРМУЛА НА МАРКАХ

На этой марке, выпущенной в ГДР в честь Леонарда Эйлера, изображен икосаэдр и формула A— C+ V = 2 в немецком варианте. Интересный способ рассказать о формуле всему свету.