Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

В формуле Декарта 1640 года и формуле Эйлера 1752 года фигурируют только грани, ребра и вершины, поэтому эти формулы применимы к множеству различных фигур и по-прежнему выполняются даже после определенных преобразований.

Эти формулы дали начало новому разделу математики — топологии, которая бурно развивалась в XIX веке. Август Фердинанд Мёбиус, Бернхард Риман, Анри Пуанкаре, Ян Брауэр, Соломон Лефшец и многие другие математики, которые работали в различных областях, нашли в этой «новой геометрии» фундаментальную основу для изучения кривых, поверхностей, пространств, функций. Топология помогла определить свойства, которые нельзя было формализовать в рамках традиционной геометрии.

Август Фердинанд Мёбиус— один из математиков XIX века, интересовавшихся топологией.

Если говорить кратко, то топология свободна от жестких структур евклидовой и проективной геометрии. С помощью «непрерывных преобразований» стало возможным моделировать новые фигуры и определять новые категории преобразований. Представим себе треугольник, нарисованный на поверхности шара. При сжатии шара (таком, что шар не ломается) треугольник будет принимать различную форму. Будут изменяться углы и длины сторон, но «сущность» треугольника будет оставаться неизменной: это по-прежнему будет фигура, определяемая тремя точками и тремя отрезками, соединяющими эти точки. Чтобы начать мыслить с топологической точки зрения, нужно представить, что все фигуры сделаны из резины и могут деформироваться. Так, деформацией сферы невозможно получить бублик, но зато бублик будет эквивалентен… чайной чашке.

Рассмотрим выпуклый п-угольник с вершинами V, V 2 ,..., V n и ребрами V 1V 2 ,..., V 2V 3 ,..., V n-1V n, V nV 1.

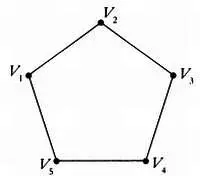
Вне зависимости от длин сторон, величин углов, кривизны ребер и прочих параметров, число ребер будет всегда равно числу вершин многоугольника. Это соотношение столь тривиально, что на него можно даже не обратить внимание. Если сохранить число вершин неизменным и заменить одно из прямых ребер любой простой кривой, это соотношение не изменится.

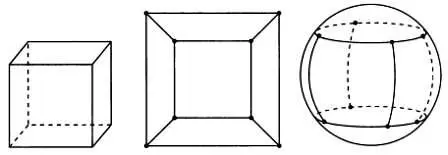
Перейдем в трехмерное пространство и рассмотрим произвольный выпуклый многогранник, который имеет V вершин, А ребер и С граней. Если посмотреть на этот многогранник изнутри и спроецировать его на большую сферу, внутри которой он находится, то на эту сферу окажутся нанесены линии и соответствующие вершины так, что значения V, А и С останутся неизменными.

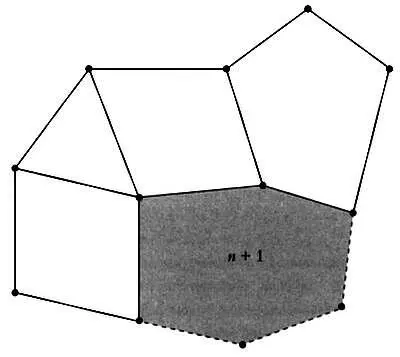
Многограннику также можно поставить в соответствие плоский граф, который будет иметь то же число ребер А , то же число вершин V и то же число граней С .

Можно заметить, что при С = 2 получится единственный многоугольник и V = А , либо, что аналогично, С + V = А + 2. Если при С — n число вершин равно V , число ребер — А n , и мы предположим (по индукции), что n + V n = А n + 2, то при С = n + 1 нужно заострить внимание на грани под номером n + 1. Когда число граней станет равным n + 1, к графу с n гранями, V n вершинами и А n ребрами добавится некоторое число вершин К и К + 1 ребро. Следовательно,

C + V n+1 = n + 1 + V n + K = ( n + V n ) + ( K + 1) = ( A n + 2) + ( K + 1) = ( A n + K + 1) + 2 = A n+1 + 2.

Так доказывается знаменитая формула Эйлера, которая звучит следующим образом: в любом выпуклом многограннике выполняется соотношение

С + V = A + 2.

Этот результат может показаться тривиальным, но если немного подумать, то мы увидим, что это соотношение поистине удивительно: оно выполняется для любого выпуклого многогранника независимо от формы его граней, углов на гранях и углов между гранями, от длин ребер и других параметров. Формула, которая выполняется для бесконечно большого числа разнообразных фигур, не может не привлекать внимание. Здесь что-то не так. Практически не существует формул, которые справедливы для столь непохожих фигур.

* * *

РАЗУМЕЕТСЯ, А = С + V — 2. МОЖНО ЛИ ВЫБРАТЬ С И V ПРОИЗВОЛЬНО?

В выпуклом многограннике С+ V = А+ 2, следовательно,

А= C+ V— 2. (1)

Какие значения могут принимать Си V? Существуют ли какие-то ограничения? Может ли быть так, что С = 1000, а V = 2? Рассмотрим, каковы же ограничения на Си V.

Очевидно, что V> 4, так как многогранника, у которого меньше четырех вершин, не существует. В каждой вершине сходятся минимум три ребра, следовательно, 3 V=< 2 А, так как каждое ребро связывает две вершины. Следовательно, 3 V=< 2 С+ 2 V— 4, откуда следует

4 =< V=< 2 С— 4. (2)

Также С> 4, так как чтобы ограничить часть пространства, требуется минимум четыре грани. Каждая грань должна иметь минимум три ребра, то есть 3 С=< 2 А = 2 С+ 2 V— 4, откуда

4 =< С =< 2V — 4. (3)

Отношения (1), (2) и (3) соответствуют выпуклым многогранникам в пространстве. Простейшие примеры многогранников, у которых число граней С>= 4, — это пирамиды и бипирамиды. Многоугольник, число ребер которого равно 2 К, и точка вне его образуют пирамиду, где С = 2 К+ 1. Для бипирамиды, которая получается, если совместить две такие пирамиды основаниями, С= 4 К.

* * *

С помощью формулы Эйлера для выпуклых многогранников можно вычислить так называемую характеристику Эйлера — Пуанкаре:

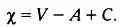
Для сферы 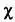= 2. Если мы рассмотрим тор (поверхность вращения, получаемая вращением окружности вокруг оси, лежащей вне этой окружности), то получим = 0. Следовательно, в тороидальных многогранниках 0 = С + V — А . Родом поверхности

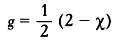
называется число отверстий в ней. Для сферы g = 0, следовательно, в тороидальных многогранниках g = 1. Итак, и g являются характеристиками поверхности, то есть число 2 в формуле С + V = А + 2 указывает на сферическую природу выпуклых многогранников. Для невыпуклых многогранников формула Эйлера не выполняется. В следующих разделах, где рассматриваются только выпуклые многогранники, мы подробно расскажем о следствиях формулы С + V = А + 2.