Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

Анализ социальных сетей использовался при изучении распространения болезней (СПИДа, малярии, туберкулеза), инноваций, анализе воздействия политических решений и даже при изучении распространения слухов.

На основе графов, с помощью которых изображаются социальные сети, вводятся количественные показатели. Многие из них используются в компьютерных программах, где изучаются, например, степени зависимости и близости, показатели централизованности, потоки между узлами, связь, эквивалентность и другие характеристики. Например, структурная связность — это минимальное число членов группы, при исключении которых она окажется отсоединенной от остальной сети. Также могут оцениваться интенсивность отношений, вероятность передачи информации, частотность взаимодействий, расстояния между узлами и другие параметры. Так, изучение централизованности помогает решать ключевые вопросы в организации — схемы передачи информации, построение иерархий, отношения лидерства. Также интересен расчет индексов влияния, уже на политическом или коммерческом уровне.

* * *

ДРУЗЬЯ ПОЛИТИКА

В математическом фольклоре эта задача известна уже много лет. Допустим, что в группе людей, состоящей как минимум из трех человек, у любых двух ее членов есть ровно один общий друг. Следовательно, всегда существует человек (так называемый политик), который будет другом всех членов группы. Пол Эрдёш и Альфред Реньи формализовали и решили эту задачу с помощью графов: если граф имеет nвершин ( n >= 3) и для любой пары вершин существует вершина, смежная им обеим, то должна существовать вершина, смежная всем вершинам графа.

* * *

«Маленький мир» Стэнли Милгрэма

В 1967 году психолог Стэнли Милгрэм провел эксперимент, подтвердивший концепцию «маленького мира». Несколько человек попросили передать сообщение (например, письмо) определенным людям по цепочке через своих знакомых. В большинстве случаев сообщение удалось передать получателю за шесть шагов. Этот эксперимент проводился неоднократно, и всякий раз число звеньев в подобных цепочках оказывалось очень малым (пять, шесть, восемь). Эта тема вновь обрела популярность с появлением гиперссылок и электронной почты.

В нашем сложном мире одним из важнейших вопросов является необходимость качественного планирования расписаний с целью оптимизации временных затрат. Все, что окружает нас, подчиняется принципу «время — деньги».

Причина оптимизации временных затрат — стремление максимально эффективно использовать персонал и оборудование в области грузоперевозок, на производстве, в сфере услуг. Ранее мы уже приводили примеры, в которых требовалось сократить интервалы между посадкой и взлетом самолета или оптимизировать выполнение строительных работ. Сейчас мы расскажем о том, как теория графов и задачи оптимизации времени используются в повседневной жизни.

Рассмотрим последовательность повседневных действий, например покупку продуктов в нескольких магазинах и приготовление ужина. При выполнении этих действий можно следовать такому алгоритму.

1. Пронумеровать все задачи и оценить сроки их выполнения.

2. Определить, какие задачи являются независимыми (например, покупка продуктов в разных магазинах), а какие нужно выполнять последовательно и в определенном порядке. На этом шаге можно построить граф, вершины которого будут обозначать задачи и время их выполнения, а дуги — указывать порядок выполнения задач.

3. В зависимости от числа людей, которые будут нам помогать, и количества используемого оборудования (духовка, миксер, скороварка и так далее) определить максимально возможное число задач, которые можно выполнять параллельно (к примеру, сервировать стол), и задачи, которые обязательно должны выполняться последовательно, но так, чтобы общее время их выполнения было минимальным.

Чтобы сократить время, необходимое для приготовления нашего роскошного ужина, можно применить алгоритм, который используется при раскраске графов: необходимо последовательно назначать исполнителей задачам, учитывая их порядковые номера, очередность и время выполнения.

На рисунке приведен пример ориентированного графа и последовательности действий при выполнении некоей задачи. Предполагается, что в условии даны две единицы оборудования, работающие параллельно.

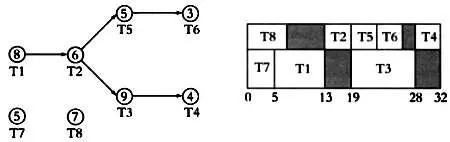
Некоторые задачи длительнее остальных, поэтому можно упорядочить задачи по убыванию времени их выполнения, то есть назначить наивысший приоритет задачам, которые выполняются дольше всего (например, жарка птицы или варка мяса), не забывая о последовательности их выполнения.

Как вы уже догадались, эта задача имеет особое значение во многих областях: при конвейерной сборке автомобилей, телевизоров, компьютеров, при печати в типографии, когда задействуется различное оборудование и несколько сотрудников, при составлении расписания операций в больнице, формировании очередей на операции, определении смен врачей скорой помощи, при распределении композиций альбома на два диска, составлении графика отпусков, графика работы персонала гостиниц и ресторанов, расписаний поездов метро, автобусов, самолетов.

Во всех этих случаях преследуется цель оптимизации времени работы с учетом соответствующих изменений расходов, качества обслуживания, эффективности работы организации и так далее.

Разумеется, порой необходимо оптимизировать не время, а другие параметры. Например, если нужно собрать чемоданы, перевезти мебель при переезде, подготовить контейнер с вещами к отправке, графы и соответствующие алгоритмы помогут оптимизировать занимаемое пространство. Так, для этого может применяться алгоритм убывания вероятности. Это интуитивно понятный алгоритм, при котором укладка начинается с тех вещей, которые занимают больше места.

* * *

МАТЕМАТИКИ И ЯИЧНИЦА

В одной из популярных юмористических историй о математиках рассказывается о том, как они пытаются оптимизировать все возможные действия, чтобы максимально снизить объем работы. Один математик подробно объяснил процесс приготовления яичницы: извлечь сковородку из шкафа, включить плиту, поставить сковородку на плиту, налить масло, дождаться, когда сковородка нагреется, разбить яйцо на сковородку, добавить соль… Этого математика спросили: «Что вы будете делать, если плита уже включена и сковородка стоит на конфорке?» Математик ответил: «Выключу плиту и уберу сковородку в шкаф, чем сведу задачу к ранее решенной».