Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

Магическая гексаграмма

Рассмотрим магическую гексаграмму. Гексаграмма — это знаменитая и легендарная Звезда Давида и Печать Соломона, образуемая наложением двух равносторонних треугольников друг на друга.

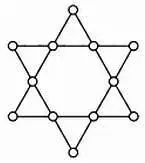
Как видно на рисунке, эта фигура имеет 12 вершин, расположенных в шесть рядов по четыре вершины, поэтому в этой задаче нужно присвоить вершинам числа от 1 до 12. Так как сумма чисел от 1 до 12 равна 78, магическая константа будет равна 78·2/6, то есть 26. Сосредоточьтесь, приготовьте карандаш и найдите одно из нескольких десятков решений этой задачи. В конце главы (стр. 122) приведено одно из возможных решений.

Если вам понравилось решать задачи с магическими звездами, попробуйте найти одно из множества возможных решений для семиконечной или восьмиконечной звезды.

Более простой альтернативой этой задаче, для которой существует строгий алгоритм решения, являются магические окружности — несколько окружностей, в точках пересечения которых нужно расположить числа так, чтобы сумма чисел на каждой окружности была одинаковой, например 20. На следующем рисунке изображены три окружности, точки пересечения которых обозначены буквами а, b, с, d, р, q . Можно записать соотношения, которые должны выполняться для чисел, соответствующих этим вершинам.

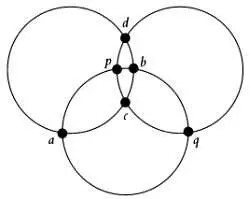
Получим систему уравнений:

a + b + c + d = 20,

с + d + р + q = 20,

а + Ь + р + q = 20.

Сложив все три уравнения, получим:

2 а + 2 Ь + 2 с + 2 d + 2 р + 2 q = 60,

или, что аналогично,

a + b + c + d + q = 30.

Вычтем из последнего равенства все три исходных равенства и получим:

a + b = c + d = p + q = 10.

Следовательно, существует множество различных вариантов, например:

а = 1, Ь = 9, с = 2, d = 8, р = 3, q = 7.

* * *

ТЕОРИЯ ИГР

Теория игр была создана Джоном фон Нейманом и Оскаром Моргенштерном с целью разработки новых моделей для решения экономических задач. Развитие этой теории позволило использовать ее не только в экономике, но и в социологии, политике, маркетинге, финансах, психологии и других областях.

Изначально создатели теории игр полагали, что «типичные задачи, в которых рассматривается экономическое поведение, полностью идентичны математическому представлению соответствующих стратегических игр». На основе этого сравнения стало возможным проанализировать игры для одного и нескольких игроков, ввести понятие функции полезности, изучить стратегии различных типов (консервативные, выигрышные и другие), коалиции и голосования, вероятностный анализ и анализ случайных процессов и так далее.

Так как в общем случае число «игроков» (инвесторов, работников, банков) является конечным, так же как и число игр, стратегий и возможных вариантов, то при анализе задач теории игр часто применяется теория графов.

* * *

Интенсивное развитие теории графов на протяжении всего XX века и ее применение во множестве самых разных задач пробудили интерес к преподаванию этой дисциплины в высшей школе.

Курс «Теория графов и ее применение» сегодня изучается как часть курса математики, исследования операций, дискретной математики, входит в программу различных инженерных специальностей (строительство, электроэнергетика, телекоммуникации) и, разумеется, в курс информатики.

Однако до сих пор не решен вопрос о преподавании теории графов в старшей школе. Речь не идет о том, чтобы изучать теорию графов в том же объеме, что и арифметику или геометрию, однако различные эксперименты в сфере образования показывают, что элементы теории графов имеют высокую образовательную ценность и должны быть включены в школьную программу.

Среди преимуществ теории графов применительно к образованию выделим следующие.

1. Графы часто представляют собой прекрасные примеры математических моделей. Несмотря на простоту графов, с их помощью можно описывать и изучать интересные реальные ситуации.

2. Графы — прекрасный пример использования математики в повседневной жизни. Они помогают увидеть, что математика постоянно присутствует в окружающем нас мире.

3. Изучение графов стимулирует индуктивное, комбинаторное и пространственное мышление, что имеет высокую образовательную ценность.

4. Графы помогают решать занимательные и прикладные задачи. Благодаря работам Дьёрдя Пойа мы знаем, что решение задач — один из двигателей обучения математике.

С учетом вышесказанного будет уместно привести цитату из «Алисы в стране чудес» Льюиса Кэрролла, где Алиса разговаривает с Котом:

«— Скажите, пожалуйста, куда мне отсюда идти?

— А куда ты хочешь попасть? — ответил Кот.

— Мне все равно… — сказала Алиса.

— Тогда все равно, куда и идти, — заметил Кот».

Путь, которым должно следовать образование, подразумевает качественное обучение для всех. Образование должно гарантировать актуальность теоретических и практических знаний. Нельзя, чтобы школьная программа ограничивалась рассмотрением задач столетней давности, чтобы в ней не рассматривались важные современные задачи.

Развитие информатики привело к тому, что многие математические модели стали использоваться в автоматических процессах (выполняемых машинами), которые, безусловно, способствуют прогрессу. Учитывая невероятную сложность человеческого мозга, модели искусственного интеллекта должны содержать нетривиальные способы обработки данных. Машина легко справляется с вычислениями, но порекомендовать один из нескольких возможных вариантов — задача намного более сложная.

На начальном этапе развития искусственного интеллекта особое внимание привлекали так называемые экспертные системы — программы, которые на основе знаний людей-экспертов могли давать рекомендации, помогающие принимать решения. Экспертные системы имели особый успех в медицине: они помогали ставить диагноз с учетом определенных параметров на основе множества реальных историй болезни. Появились и другие алгоритмы, например генетические, в которых используются механизмы, напоминающие биологическую эволюцию. В генетических алгоритмах случайные ситуации обрабатываются статистическими методами и влияют на алгоритм решения конкретной задачи. Эти алгоритмы применяются в эволюционном и генетическом программировании. Графы в них используются как способ визуализации процессов. В свою очередь, эти алгоритмы, которые можно встретить в различных системах, сетях, в задачах прогнозирования и других, также связаны с теорией графов, теорией игр и логикой.