Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

Реальный мир сложен, на события и явления влияет множество факторов, но иногда искусство упрощения, умение устранить второстепенные детали и заострить внимание на наиболее важном — лучший способ разобраться в сути проблемы. Возможно, сила, заключенная в простоте графов, напоминает путь развития искусства в XX веке. Вместо того чтобы следовать по пути гиперреализма или вычурного барокко, в живописи и скульптуре была заново открыта художественная ценность цветных точек, линий и простых геометрических фигур. Современное искусство показывает, как можно с помощью простейших фигур и основных цветов создать художественные коды, новые эстетические каноны и передать эмоции.

Теория графов — еще одно подтверждение того, как важно уметь видеть лишь основное и необходимое в сложном мире.

В завершение эпилога приведем некоторые размышления философов на тему того, почему наше пространство имеет три измерения. Много лет назад Джеральд Джеймс Уитроу в своей книге «Структура и эволюция Вселенной» показал, что в пространствах, имеющих больше трех измерений, стабильное и равномерное движение планет вокруг Солнца было бы невозможно. Но в двумерном пространстве разумная жизнь также не могла бы существовать, что доказывает теория графов: мозг состоит из огромного числа нейронов (вершин графа!), связанных между собой нервами (ребрами графа!), которые не должны пересекаться. Подобные сложные связи между нейронами в двумерном пространстве были бы невозможны, что ясно видно на примере плоских графов. Эта аналогия особенно интересна тем, что даже наш разум представляется в ней как огромный нейронный граф.

Желаем, чтобы прекрасные графы сопровождали вас по жизни и помогали в решении самых разных задач.

Математика, подобно любому прочному зданию, твердо стоит на фундаменте. Логика играет главную роль при выполнении дедуктивных умозаключений, лежит в основе понятий истинности и ложности, различий между аксиомами (постулатами) и теоремами, допустимыми формами доказательств и так далее. Теория множеств — еще одна колонна, на которой стоит здание математики. С ее помощью можно формализовать самые основные составляющие математических структур: элементы, множества, отношения, функции.

В наглядных объяснениях теории множеств используются как символы, так и графические обозначения. 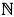= (1, 2, 3, …} обозначает множество натуральных чисел. На рисунке ниже изображено это же множество в виде точек на прямой.

* * *

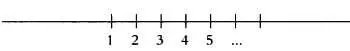
ГЕОРГ КАНТОР (1845–1918) И ТЕОРИЯ МНОЖЕСТВ

Этот гениальный немецкий математик создал теорию множеств, чтобы дать более строгие определения многим математическим понятиям, в частности понятию бесконечности. Важный вклад в теорию множеств также внесли Фридрих Фреге и Юлиус Дедекинд. Благодаря Кантору стало возможным говорить, что «конечное множество — это множество, которое не является бесконечным» и что множество А является бесконечным, если между этим множеством и его подмножеством можно установить взаимно однозначное соответствие, то есть один к одному. Кантор прояснил вопрос, касающийся счетных бесконечных множеств, например множеств натуральных, целых или дробных чисел. Ему же принадлежит определение различных категорий бесконечностей (трансфинитные кардинальные и ординальные числа). Его идеи породили ожесточенные споры с другими математиками того времени (его основным противником стал Леопольд Кронекер), появились некоторые парадоксы, которые требовалось разрешить. Однако благодаря ему родилась красивая и фундаментальная теория множеств.

* * *

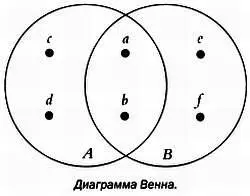
Для конечных множеств А = { a, b, с, d }, В = { а, Ь, е, f } обычно используются диаграммы Венна. На этих диаграммах элементы множеств представлены в виде отдельных точек и замкнутых кривых, ограничивающих группы точек.

Для множеств А, В их декартово произведение А x В определяется так:

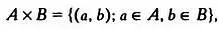
то есть как множество упорядоченных пар ( а, Ь ). Это обозначение связано с традицией, начатой Рене Декартом, обозначать точки на плоскости ( х, у ) или в пространстве ( х, у, z ) упорядоченными парами или тройками чисел — координатами. Заметим, что слова по сути тоже представляют собой упорядоченные множества букв.

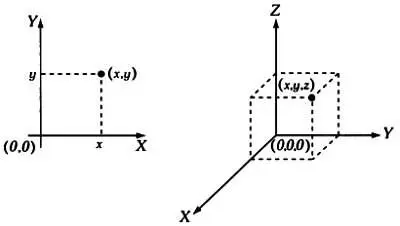
Декартовы координаты на плоскости и в пространстве.

На основе декартовых произведений вида А x A , то есть произведений множества на само себя, можно определить базовое понятие отношения R как подмножества А х А . Иными словами, отношение указывает элементы А , связанные между собой.

Если ( а, Ь ) принадлежит R , то между а и Ь имеется отношение. Если ( а, с ) не принадлежит R , то между а и с отсутствует отношение. Так, для данного отношения R для каждого элемента а имеет смысл рассматривать класс всех элементов, для которых установлено отношение с а . Если ( а, Ь ) принадлежит R , то это отношение также записывается в форме « а R Ь ».

Рассмотрим в качестве примера множество А = {2, 3, 4, 5, 6, 7, 8, 9, 10} и отношение R на множестве A: a R Ь , если а кратно Ь . Упорядоченные пары для этого отношения можно представить в декартовых координатах.

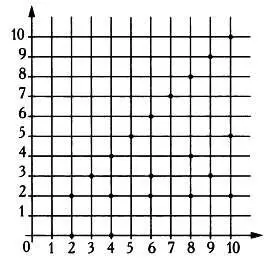
Представление отношения в декартовых координатах.

Также можно использовать ориентированный граф, как показано ниже:

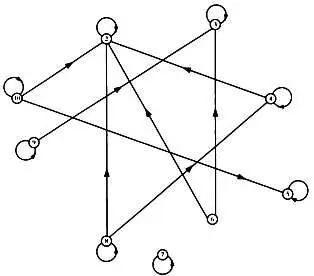
Направленный граф, представляющий отношение.

Отношения эквивалентности

Применительно к классификациям на множестве особый интерес представляют так называемые отношения эквивалентности R на множестве А . Они обладают тремя свойствами.

1. Рефлексивностью: a R а .

2. Симметричностью: если a R Ь , то b R а .

3. Транзитивностью: если a R b и b R с , то a R с .