Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

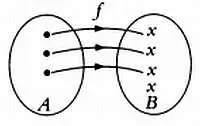
Инъективное отображение.

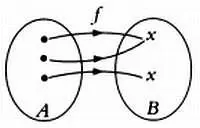
Сюръективное отображение.

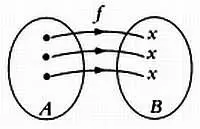
Биективное отображение.

Чтобы найти все возможные отображения конечного множества А на множество В , будет полезно использовать графы, которые являются деревьями.

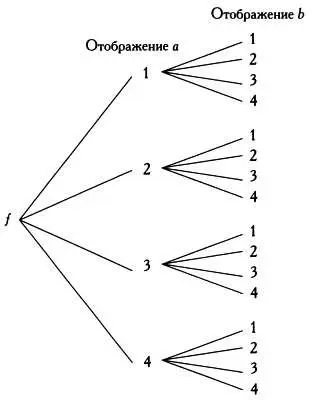
Дерево возможных отображений множества A= { a, b} на множество B = {1, 2, 3, 4}.

Если даны два отображения — отображение f множества А на множество В и отображение g множества В на множество С , то имеет смысл говорить о композиции отображений f и g множества А на множество С , то есть о присвоении каждому элементу а множества А элемента g ( f( а )) множества С . Композиции отображений g и f обозначается как gо f . Ее можно представить в виде графов следующего вида.

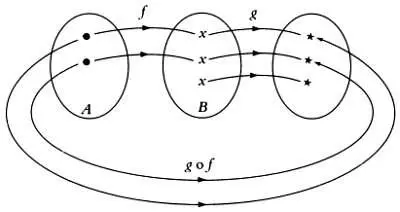
Граф композиции отображений qи f.

Нечеткие множества и графы

В последние десятилетия в целях моделирования сложных ситуаций реальной жизни все шире применяется теория нечетких множеств, созданная инженером Калифорнийского университета в Беркли Лотфи Заде. В классической трактовке элемент а либо принадлежит множеству А , либо нет. Следовательно, множество определяется характеристической функцией: она принимает значение 1 для элементов, принадлежащих A , и 0 для элементов, не принадлежащих A .

Идея Заде состояла в том, чтобы расширить характеристические функции и создать нечеткие множества, то есть определить функции, которые ставят в соответствие элементам x универсального множества X значения f( х ) в интервале от 0 до 1. В такой трактовке f( х ) определяет степень принадлежности х к А .

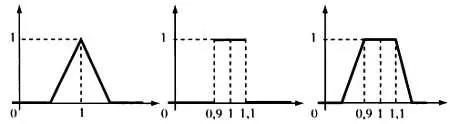
Нечеткие множества, соответствующие утверждению «результат примерно равен 1».

* * *

ЖУРНАЛЫ О ДИСКРЕТНОЙ МАТЕМАТИКЕ, КОМБИНАТОРИКЕ И ГРАФАХ

Ниже перечислены ведущие современные журналы по этим темам.

· Ars Combinatorica.

· European Journal of Combinatorics.

· Combinatorica.

· Geombinatorics.

· Combinatorics, Probability and Computing.

· Journal of Algebraic Combinatorics.

· Designs, Codes and Cryptology.

· Journal of Combinatorial Theory. Series A.

· Discrete and Computational Geometry.

· Journal of Combinatorial Theory. Series B.

· Discrete Applied Mathematics.

· Journal of Geometry.

· Discrete Mathematics.

· Journal of Graph Theory.

· Electronic Journal of Combinatorics.

* * *

Одному и тому же расплывчатому понятию можно сопоставить разные нечеткие множества. Именно это и вызывает интерес к теории нечетких множеств — она допускает альтернативные трактовки одной и той же ситуации. Задачи искусственного интеллекта, управления механизмами, обработки цифровых фотографий, распознавания образов и другие задачи (даже стиральные машины с нечеткой логикой) — прекрасные наглядные примеры того, как эта теория используется на практике. Введение степеней — очень важная идея, ведь между черным и белым существует множество оттенков серого.

В рамках теории нечетких множеств также рассматриваются нечеткие классификации и упорядоченность; можно говорить о степенях отношений. Эта теория основана на теории множеств и может быть подтверждена примерами из теории вероятностей (вероятность является оценкой какого-либо события и лежит в интервале от 0 до 1), но особенно интересна в эмпирических моделях и при решении задач, на которые нельзя дать четкого и однозначного ответа в рамках классической математики.

В частности, в теории нечетких множеств тоже используются графы отношений, но в этом случае значения от 0 до 1, присваиваемые парам элементов, сопоставляются ребрам графов. Иными словами, получается взвешенный граф.

Мы надеемся, что в этом разделе нам удалось показать, что теория графов также может быть сформулирована в терминах теории множеств и что графы играют важную роль даже при построении графиков.

Алгоритм— пошаговая последовательность действий по решению задачи.

Вершина— точка графа, где сходится одно или более ребер; также может быть изолированной.

Вес— значение, поставленное в соответствие ребру графа, означающее стоимость, расстояние, время и пр.

Взвешенный граф— граф, каждому ребру которого поставлено в соответствие некоторое число.

Гамильтонов граф— граф, в котором существует гамильтонов цикл.

Гамильтонов цикл— цикл, содержащий все вершины графа ровно по одному разу.

Гомеоморфные графы— графы, один из которых получается из другого путем добавления или удаления вершин степени 2. Если в таких графах удалить все вершины степени 2, полученные графы будут одинаковыми.

Грань— область, ограниченная ребрами плоского графа.

Граф— совокупность множества точек (вершин) и линий (ребер), соединяющих некоторые точки.

Дерево — связный граф, не содержащий циклов.

Дуга— ориентированное ребро графа. Изображается стрелкой.

Изоморфные графы— графы, между вершинами и ребрами которых существует взаимно однозначное соответствие, которое сохраняет смежность и инцидентность.

Критический путь— путь максимальной длины в ориентированном графе.

Лес— множество графов, которые являются деревьями.

Матрица инцидентности графа— матрица n x n чисел, элементы которой равны 1, если между соответствующими вершинами имеется ребро, и 0 в противном случае.

Метка— информация, присвоенная вершинам и ребрам графа; например, числа, слова, наименования.

Оптимальное решение— наилучшее решение (согласно некоему количественному показателю) из множества возможных решений.

Органиграмма— граф, упорядочивающий информацию, устройство организации или действия, которые необходимо выполнить для решения задачи.

Орграф( ориентированный граф) — граф, все ребра которого являются ориентированными, то есть дугами.