Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

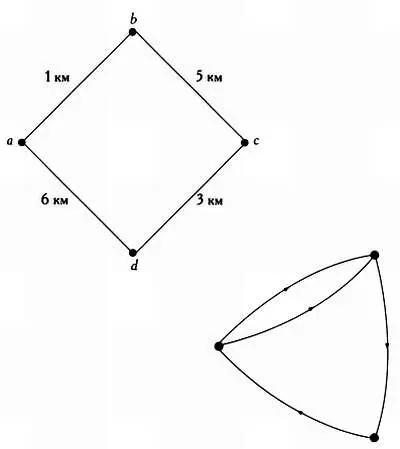
Если вершинам графа сопоставить буквы, числа или некую другую информацию, то говорят, что такой граф является помеченным. Если ребрам графа поставлены в соответствие некие веса, такой граф называется взвешенным. Если на ребра графа нанести стрелки, обозначающие направления, то эти ориентированные ребра графа будут называться дугами. Если все ребра графа являются ориентированными, то такой граф называется ориентированным, или орграфом.

Графы также можно представить в виде списков, таблиц и различных выражений. Вершины графа можно изобразить в виде точек, окружностей, треугольников, а ребра — в виде прямых отрезков или фигурно изогнутых линий. Учитывая подобное разнообразие, важно уметь определять, когда два представления графа являются эквивалентными (изоморфными). Эквивалентные представления графа содержат одинаковые вершины и одинаковые связи между ними. Иными словами, между вершинами и ребрами двух представлений должно существовать взаимно однозначное соответствие, такое что степени вершин в обоих случаях будут одинаковы.

Три следующие фигуры — это три разных представления одного и того же графа. Согласитесь, увидеть это не так-то просто!

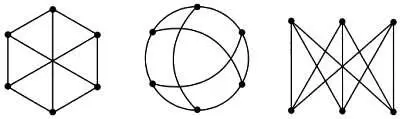
На рисунках ниже изображены четыре графа — ( а ), ( Ь ), ( с ) и ( d ). Граф ( а ) является исходным, остальные три — его подграфы. Это означает, что в них были выбраны лишь некоторые ребра и вершины исходного графа. Подграфы позволяют изучать графы по частям.

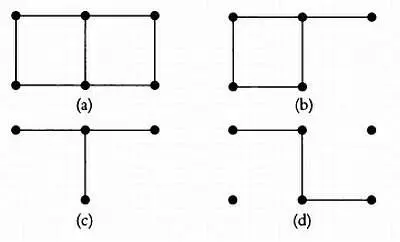
Обычно различают три типа графов: обыкновенные графы, мультиграфы и псевдографы. На рисунках ниже слева направо представлены все три типа графов.

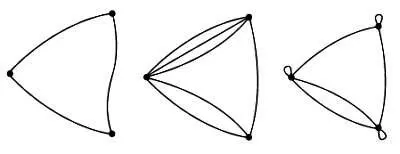
В обыкновенном графе две вершины могут соединяться только одним ребром. Если они соединены более чем одним ребром, то такой граф называется мультиграфом. Если вершина мультиграфа может соединяться сама с собой, то такой граф называется псевдографом. Ребро, начало и конец которого находятся в одной вершине, называется петлей. В этой книге все три типа графов мы будем называть просто графами, уточняя возможные ограничения в каждом конкретном случае.

Применительно к различным вариантам обхода графа используются следующие обозначения. Пусть G — помеченный граф с вершинами V 0, V 1, V 2, . и ребрами X 1, Х 2, Х 3 , … Тогда маршрутом в графе G будет называться конечная последовательность вида V 0, X 1, V 1, ., V n-1, X n, V n , в которой чередуются ребра и вершины. Запись вида ( V 0, V 1 , …, V n ) подразумевает, что любые две вершины соединяются только одним ребром, и маршрут определяется указанной последовательностью вершин. Если V 0 = V n , то есть исходная и конечная вершина маршрута совпадают, то маршрут является замкнутым, иначе — открытым. Путь — это маршрут, в котором каждое ребро проходится только один раз. Замкнутый маршрут, содержащий п разных вершин, называется циклом. Обратите внимание, что любой цикл можно представить графически в виде многоугольника, что будет показано позже.

* * *

ГРАФЫ И ГРАФИКИ

Граф. Это слово может означать «пишу» («графология», «графомания», «телеграф»), а в случае теории графов обозначает множество точек и линий между ними. Не следует путать графы и графики. Да, можно заметить, что в графиках линейных функций, образованных прямыми линиями или последовательностью отрезков, соединяющих точки, фактически каждой точке хоси ОХсопоставлена точка ( х, f( x)) на графике функции. Это выполняется и в классических графиках функций, построенных в декартовых координатах с двумя осями Xи Y, на которых отмечаются точки ( х, f( x)), образующие график функции у = f( х). Тем не менее это множество точек и линий нельзя назвать графом.

Графы обычно используются для представления отношений между элементами конечного множества. Например, чтобы представить отношения эквивалентности, позволяющие разделить элементы множества на классы, «точками» графа изображают элементы множества и соединяют «линиями» связанные или эквивалентные элементы (если элемент связан сам с собой, то на графе образуется петля). Отношения порядка изображаются с помощью ориентированных графов. Дуги со стрелками означают отношение «меньше, чем». Связь теории графов и теории множеств более подробно объясняется в Приложении.

* * *

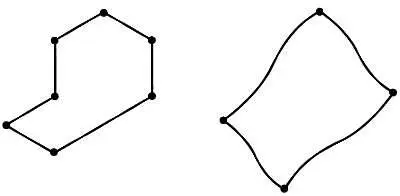
Если между любыми двумя вершинами графа можно провести маршрут, то говорят, что граф является связным, как в случаях, представленных на рисунках выше. Для связных графов имеет смысл определить расстояние между вершинами u и v как минимальное количество ребер, образующих маршрут между u и v .

В приведенных выше двух примерах на рисунке слева изображен связный граф, на рисунке справа — несвязный.

* * *

ГРАФЫ И ЧИСЛА

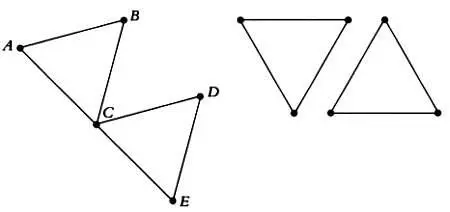
Если две вершины графа могут соединяться не более чем одним ребром, то такой граф можно выразить таблицей чисел, или матрицей. Связный граф ABCDE , изображенный на рисунке, можно представить в виде следующей таблицы. Если соответствующие вершины соединены ребром, в ячейке записывается 1, если нет — 0.

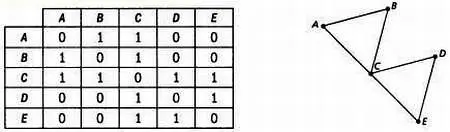
ПЕРЕДАЧА СООБЩЕНИЙ И ОШИБКИ

В 1956 году Клод Шеннон, создатель теории информации, занялся проблемами передачи сообщений по каналам связи, где сигнал может искажаться. В подобных задачах канал связи представляется в виде графа: его вершины соответствуют символам сообщения, а ребра соединяют вершины, соответствующие символам, которые можно перепугать между собой при передаче данных.

* * *

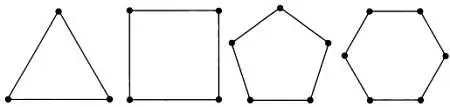
Циклы — это очень простые маршруты, проходящие через все вершины, начальная и конечная точка которых совпадают. Примеры циклов представлены на следующих рисунках.

Подобными графами можно представить маршруты городских автобусов или маршруты патрулей. Число вершин V равно числу ребер А .