Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

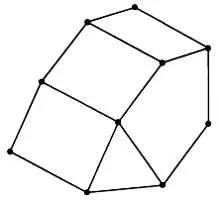
Совокупность циклов образует так называемый геометрический граф — плоскую фигуру из вершин (точек плоскости) и ребер (линий, соединяющих некоторые пары вершин). Область, ограниченная ребрами и не содержащая внутри себя вершин и ребер графа, называется гранью. Подсчитать общее число вершин V и число ребер А несложно.

При подсчете числа граней С следует учитывать, что внешняя часть плоскости также образует грань, так как она тоже ограничена циклом из вершин и ребер графа. Таким образом, граф, изображенный на следующем рисунке, имеет 10 вершин, 14 ребер и 6 граней.

Графы, в которых любая пара вершин соединена ребром, называются полными. На следующих рисунках приведены полные графы с числом вершин от 2 до 7. Полный граф с n вершинами обозначается К n .

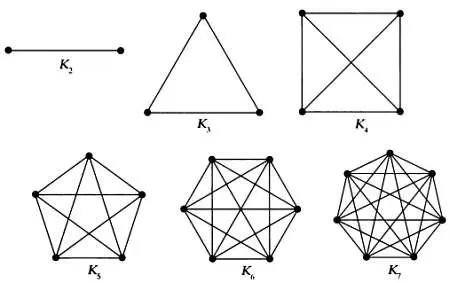
Подсчитать число ребер полного графа К n очень просто: каждая вершина должна соединяться с n — 1 вершиной, число вершин равно n , следовательно, значение выражения n ( n — 1) будет равно удвоенному числу ребер (так как каждое ребро соединяет две вершины). Поэтому общее число ребер будет равно n ( n — 1)/2 — биномиальному коэффициенту 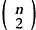, равному числу всех возможных пар на множестве из n элементов. Зависимость между числом ребер и n является квадратичной, следовательно, число ребер К n будет возрастать очень быстро.

* * *

ТЕОРЕМА ТУРАНА

В 1941 году Пал Туран поставил следующую задачу. Пусть дан простой граф Gс nвершинами, число р( р>= 2) — число вершин полного р-вершинного подграфа графа G (иными словами, К р). Вопрос таков: каково максимальное число ребер графа, который не содержит подобный р-вершинный подграф? Удивительно, но число ребер не может быть больше, чем n 2 р/2( р-1). Эта теорема и ее очень красивое доказательство занимают важное место в теории графов.

* * *

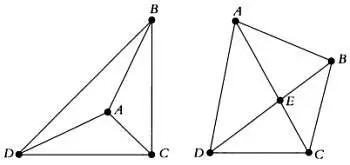
Определив вершины графа, их можно соединить ребрами так, как показано на следующих рисунках.

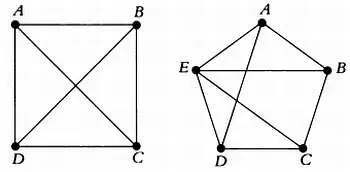
Однако эти графы можно изобразить иначе: сохранить прежние связи между вершинами, но избежать пересечений ребер в точках, которые не являются вершинами графа, как в двух предыдущих случаях. Новые изображения представлены на следующих рисунках:

Граф называется планарным, если его можно изобразить на плоскости так, что его ребра будут пересекаться только в вершинах графа (такое изображение называется плоским графом). Заметим, что для анализа планарности графа нужно определить, существует ли эквивалентный (изоморфный) ему граф, который можно изобразить без ненужных пересечений ребер. Было бы очень удобно, если бы все графы были планарными. Но так ли это? Прежде чем приступить к поискам ответа на этот вопрос, подумаем над самой известной задачей занимательной математики, посвященной графам.

* * *

ЭЛЕГАНТНЫЕ ПЛОСКИЕ ГРАФЫ

Не следует думать, что ребра плоского графа должны иметь какую-то причудливую форму. Любой плоский граф можно изобразить так, что его ребра будут отрезками и эти отрезки будут пересекаться только в вершинах графа. Сложно представить что-то более элегантное.

* * *

Задача звучит так: в трех домах а, Ь, с живут три семьи, враждующие между собой. Рядом с их домами находятся три колодца е, f, g . Один из колодцев всегда полон, два других пусты. Соседи хотят проложить дорожки так, чтобы из каждого дома можно было попасть к каждому колодцу. Никакие две дорожки не должны пересекаться, чтобы каждый мог избежать встреч с соседями. Можно ли проложить девять дорожек таким способом?

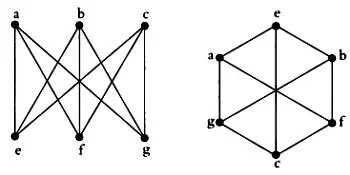
На рисунке слева показана первая попытка соединить дома а, Ь, с и колодцы е, f, g . Такой граф обозначается К 3,3 . Получилось множество нежелательных пересечений. На рисунке справа тот же граф изображен иначе, но избежать пересечений по-прежнему не удалось. Заметим, что если убрать дорожку от дома Ь к колодцу g , то можно проложить восемь дорожек без пересечений, как показано на двух следующих рисунках.

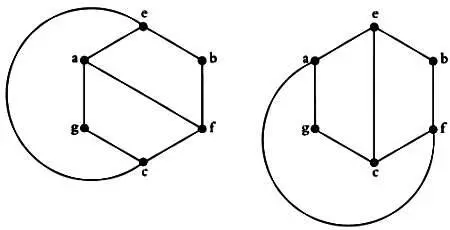
Можно ли добавить к этому графу недостающее ребро так, чтобы не пересекать остальные? Будет уместно привести одно интуитивно понятное утверждение (любопытно, что доказать его непросто): если простая плоская замкнутая непрерывная кривая делит плоскость на две части (внешнюю и внутреннюю), то любая непрерывная кривая, соединяющая точку внешней части и точку внутренней части, пересечет данную кривую минимум один раз. Это утверждение носит название теоремы Жордана. Посмотрим снова на рисунок выше и увидим, что в обоих случаях точка g находится внутри непрерывной замкнутой кривой, а точка Ь — вне ее.

Следовательно, задача о колодцах не имеет решения. Единственный способ, которым можно проложить дорожку из дома Ь к колодцу g — это построить мост, проходящий поверх одной из дорожек.

В задаче о колодцах представлен первый пример непланарного графа. Граф, который мы обозначили К 3,3 , не является планарным. Еще один простой пример непланарного графа — это полный граф К 5 в форме пятиугольника с пятиугольной звездой внутри, изображенный на рисунке:

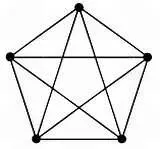
Дальше все будет только усложняться. Графы К 3,3 и К 5 не являются планарными, и если мы добавим к ним еще несколько ребер и вершин, то полученные графы также не будут планарными — этому будут мешать излишние пересечения ребер. Таким образом, можно привести бесконечно много примеров непланарных графов. Благодаря теореме, открытой Куратовским, нас ожидает приятный сюрприз. Заметим, что два графа называются гомеоморфными, если после удаления всех вершин степени 2 полученные графы будут идентичными или изоморфными. Теорема Куратовского звучит так: