Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

Площадь произвольной территории, например Китая, можно представить как сумму площадей «прямоугольных» областей, ограниченных меридианами и параллелями. Чем меньше будут эти области, тем точнее мы сможем вычислить площадь искомой территории.

Проекции, сохраняющие площади, называются равновеликими, или гомолографическими. Следовательно, мы доказали, что отображения сферы на плоскость, сохраняющие расстояния (или длины кривых), оставляют неизменными площади, геодезические линии и величины углов — все интересующие нас метрические параметры.

Учитывая вышесказанное, можно сделать вывод: чтобы построить точную карту мира, нужно найти математическую проекцию сферы на плоскость, которая была бы изометрической. Приступим же к поискам.

Теперь, говоря о точной карте земного шара или его части, мы будем знать, что это означает и что требуется для построения такой карты. Остановимся и подумаем, какой должна быть корректная проекция земной сферы на плоскость, то есть изометрическая проекция, сохраняющая все интересующие нас метрические свойства. Логично предположить, что искомую карту следует составить на основе фотографий, сделанных с самолета или спутника.

Спутниковый снимок Европы.

Может показаться удивительным, но карты, созданные на основе спутниковых снимков, неточны: они не сохраняют ни одно из метрических свойств, указанных выше. Для нашей задачи не имеет значения величина ошибки, возникающая при построении этих карт. Более того, нас интересует адекватное изображение Земли из космоса, которое (если говорить о карте мира) напомнит, что Земля имеет круглую форму (работая с некоторыми картами Земли, мы забываем об этом). На спутниковых снимках земная поверхность представлена в центральной (перспективной), или сценографической проекции. Эта проекция не является изометрической, так как меридианы в ней не изображаются прямыми линиями, следовательно, эта проекция не сохраняет геодезические линии. Она также не сохраняет углы, так как проекции меридианов и параллелей не пересекаются под прямыми углами. Аналогично можно показать, что проекция не сохраняет и площади и, как следствие, не сохраняет длины кривых и расстояния.

Наша попытка построить точную карту с использованием сценографической проекции провалилась. Продолжим поиски изометрических проекций сферы на плоскость. Мы можем строить различные картографические проекции, сначала геометрически, затем — алгоритмически, пока не получим изометрическую проекцию, которая позволит создать заветную совершенную карту Земли. Это всем известный метод проб и ошибок, который имеет свои недостатки. В частности, число вариантов, которые потребуется рассмотреть, будет очень большим или даже бесконечно большим.

Вместо того чтобы создавать картографические проекции напрямую, изучать их свойства и отвергать их, если они окажутся неизометрическими (найти такую проекцию будет равносильно поискам иголки в стоге сена), попробуем несколько сузить поле поиска. Для этого сначала рассмотрим, достаточно ли построить отображение сферы на плоскость, которое априори сохраняет только один из параметров, рассмотренных выше, то есть только углы, только площади или только геодезические линии.

С формальной точки зрения это равносильно тому, чтобы ответить на вопрос: являются ли отношения следования, обозначенные стрелками на диаграмме на странице 58, отношениями эквивалентности? Иными словами, возможно ли, чтобы все преобразования, сохраняющие величины углов (конформные проекции), также сохраняли расстояния, то есть являлись бы изометрическими? Будет ли аналогичное утверждение справедливо для площадей и геодезических линий?

С практической точки зрения это упростит задачу, так как мы сможем ограничиться рассмотрением исключительно конформных проекций (то есть равновеликих проекций и проекций, сохраняющих геодезические линии). Иными словами, нас будет интересовать только сохранение одного из упомянутых геометрических атрибутов.

* * *

ПЕРСПЕКТИВНАЯ ПРОЕКЦИЯ

Эта проекция была известна древним грекам и египтянам более 2 тысяч лет назад, однако не вызывала особого внимания до XVIII века, за исключением частных случаев этой проекции: ортографической, стереографической и гномонической. Если центр проекции лежит на вертикальной линии, проходящей через центр Земли, такая проекция называется вертикальной, в противном случае — наклонной. В этой проекции центральный меридиан и центральная параллель представлены в виде прямых, а все остальные меридианы и параллели изображаются в виде прямых, дуг окружностей, эллипсов и даже парабол и гипербол в зависимости от вида проекции (полярная, экваториальная или наклонная). В этой проекции не сохраняются метрические свойства. Искажения вблизи центра малы, у краев карты — велики. Проекция практически не использовалась, за исключением случаев, когда требовалось изобразить вид Земли из космоса. С началом космической гонки в середине XX века перспективная проекция вызвала определенный интерес, так как изображения Земли и других планет стали составляться с использованием именно этой проекции. Карты с прогнозом погоды, которые мы видим в газетах и на телевидении, обычно изображаются в наклонной перспективе. Эта же перспектива используется в компьютерных изображениях и на фотографиях в интернете, в частности в программе «Google Планета Земля» ( Google Earth ).

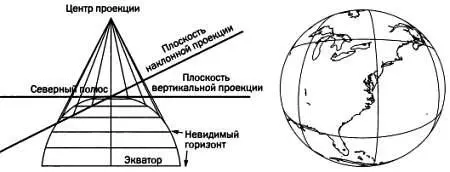
Слева — схема перспективной проекции (вертикальной или наклонной). Справа — карта, выполненная с использованием вертикальной перспективной проекции.

* * *

В следующих главах мы продемонстрируем некоторые конкретные примеры конформных и равновеликих проекций, а также проекций, сохраняющих геодезические линии, и увидим, как они изменяют различные метрические свойства. Так мы сможем определить, существует ли проекция, позволяющая составить точную карту Земли, а также рассмотрим три примера известных старинных карт мира, сохраняющих углы, площади и кратчайшие пути. В частности, вы познакомитесь с проекцией Архимеда, сохраняющей площади, центральной, или гномонической проекцией, сохраняющей геодезические линии, и стереографической проекцией, сохраняющей углы. Однако ни одна из этих трех проекций не является изометрической. Как следствие, мы не сможем ограничиться рассмотрением исключительно конформных проекций (равновеликих проекций или проекций, сохраняющих геодезические линии).