Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

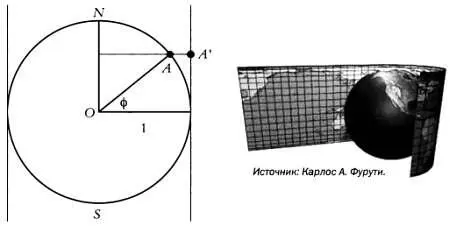
В равновеликой цилиндрической проекции Ламберта точки земной сферы горизонтально проецируются на поверхность цилиндра, касающегося сферы. Затем цилиндр разрезается по меридиану и разворачивается на плоскости.

* * *

ИОГАНН ГЕНРИХ ЛАМБЕРТ (1728–1777)

Иоганн Генрих Ламберт родился в немецком городе Мюльхаузен в провинции Эльзас (в настоящее время — Мюлуз, Франция), куда члены его семьи переехали по религиозным причинам: они были кальвинистами. В 12 лет Ламберту пришлось оставить школу и помогать отцу-портному, но в свободное время Ламберт продолжал учиться самостоятельно. Позднее он работал клерком в сталелитейной мастерской, а в 1746 году занял должность частного секретаря швейцарского философа Исаака Изелина(1728–1782) в Базеле. Двумя годами позже он стал преподавателем в доме графа Питера фон Салиса в Куре. В этой должности у него оставалось достаточно свободного времени, чтобы заниматься математикой, астрономией и философией, а также пользоваться книгами из превосходной графской библиотеки.

Ламберт был исключительным математиком: он доказал иррациональность числа πи предположил, что числа еи πтрансцендентны, то есть их нельзя представить как корни многочлена с целыми коэффициентами. Он одним из первых изучил проблему, связанную с пятым постулатом Евклида. Ламберт предположил, что пятый постулат ложен, и получил результаты, относящиеся к неевклидовой геометрии. Он занимался гиперболическими функциями, проводил важные исследования в сферической геометрии, картографии и науке о перспективе, а также совершил важные открытия в теории вероятностей. Интересы Ламберта не ограничивались исключительно математикой: он также был автором важных работ по физике, астрономии и философии.

* * *

Если мы примем радиус земной сферы равным единице и будем считать, что цилиндр касается ее в точках, лежащих на экваторе, то ось цилиндра будет проходить через Северный и Южный полюса. После построения проекции сферы на поверхность цилиндра он разрезается по меридиану и разворачивается на плоскости. Эта развертка цилиндра на плоскости является изометрической и сохраняет все интересующие нас метрические свойства. Первую карту мира в этой проекции составил Иоганн Генрих Ламберт в 1772 году.

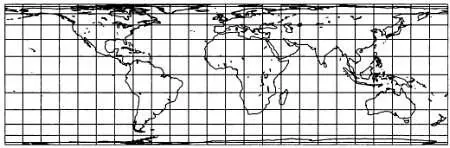
Карта, выполненная в равновеликой цилиндрической проекции Ламберта(1772).

Далее перечислены некоторые свойства карты, выполненной в равновеликой цилиндрической проекции Ламберта.

1. Она имеет прямоугольную форму, как и все карты, выполненные в цилиндрических проекциях.

2. Меридианы и параллели отображаются как прямые, они имеют равную длину (но не равны между собой) и перпендикулярны друг другу.

3. Меридианы распределены равномерно вследствие того, что масштаб во всех точках каждой параллели постоянен, однако масштабы на разных параллелях отличаются. Параллели распределены неравномерно и сближаются друг с другом по мере приближения к полюсам.

4. Так как проекция является равновеликой, она сохраняет площади (с учетом коэффициента масштаба поверхности). Этот коэффициент возникает при уменьшении размеров земной сферы (то есть при гомотетии) и постоянен во всех точках карты. Однако величины углов и геодезические линии не сохраняются.

3. Искажение форм, углов и расстояний вблизи экватора очень мало и растет по мере приближения к полюсам.

Вернемся к основному вопросу этой главы — как изменяются площади, углы и геодезические линии в равновеликой цилиндрической проекции Ламберта? Чтобы доказать, что эта проекция сохраняет площади, достаточно показать, что она сохраняет площади «прямоугольных» (достаточно малых, то есть бесконечно малых) участков, сторонами которых являются меридианы и параллели.

Как показано на следующем рисунке, для данной точки сферы на широте φ отображением меридиана (достаточно малого) длины l будет отрезок прямой на поверхности цилиндра длиной l' = l ·cos φ , а отображением параллели (достаточно малой) длины k будет дуга окружности на поверхности цилиндра, длина которой будет равна k' = k /cos φ . Следовательно, бесконечно малый «прямоугольник» с основанием k и высотой l на поверхности сферы, площадь которого равна l · k , преобразуется в «прямоугольник» с основанием k' = k /cos φ и высотой l' = l ·cos φ . Площадь полученного прямоугольника также будет равна l · k . Как следствие, проекция Архимеда сохраняет площади неизменными.

Напомним, что в этой книге мы приводим только интуитивно понятные доказательства в духе классической геометрии. Более строгое доказательство требует использования дифференциальной геометрии и методов математического анализа.

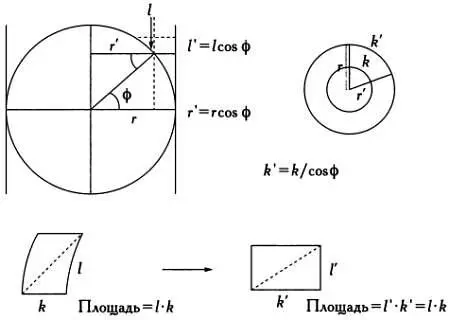
Проекция Архимедаявляется равновеликой.

Тем не менее величины углов на карте, выполненной в проекции Ламберта, не сохраняются. Чтобы убедиться в этом, посмотрите на предыдущий рисунок. В силу искажений меридианов (они сжимаются) и параллелей (они расширяются) угол между основанием и диагональю прямоугольника на сфере будет больше, чем этот же угол в проекции прямоугольника на плоскость. Однако прямые углы между меридианами и параллелями сохраняются. Из вышеизложенного можно сделать вывод о необходимых и достаточных условиях сохранения величин углов.

1. Должны сохраняться углы между меридианами и параллелями (эти углы прямые, то есть равны 90°).

2. Искажение в направлении меридианов μ должно быть равно искажению в направлении параллелей λ .

По теореме Пифагора, если оба этих свойства выполняются, то искажения в любом направлении всегда будут одинаковыми. В частности, мы показали, что для равновеликой цилиндрической проекции Ламберта искажение в направлении меридианов равно μ = cos φ , искажение в направлении параллелей — λ = 1/cos φ , а круг, центром которого является точка на сфере, в этой проекции преобразуется в эллипс на плоскости, вытянутый в направлении «запад — восток». На следующей иллюстрации изображены эллипсы, построенные в различных участках Земли, которые позволяют увидеть искажения на различных широтах.

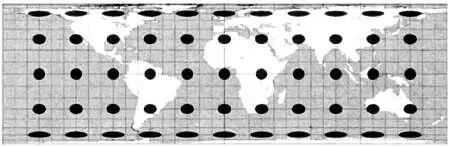
Индикатриса Тиссо, или эллипс искажения — один из способов графического изображения искажений на карте. В разных участках земной поверхности строятся небольшие окружности, после чего по их проекциям на карте можно увидеть проективные искажения в различных участках карты. Так, если мы примем радиус окружности равным λ, она преобразуется в эллипс, длины полуосей которого будут равны λи μ. Если λ = μ, то эллипсы примут форму окружностей, а отображение будет конформным. При λ= 1/ μотображение будет равновеликим. На иллюстрации представлена индикатриса Тиссо для равновеликой цилиндрической проекции Ламберта.