Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— Ничего не понял! — воскликнул Илюша.

— Прекрасно! — отвечал Радикс. — Начнем сначала. Ты знаешь, что такое четные числа?

— Ну конечно. Это те, которые делятся на два.

— Верно. А нечетные?

— 207 —

— Ну, которые на два не делятся: три, пять, семь и так далее.

— Приятно слышать. Какой милый, догадливый мальчик! Так вот, Мишкина задачка, а также задачка с бесконечной гостиницей заключаются вот в чем. Если взять все числа, то есть четные и нечетные, ведь это будут все натуральные числа, не правда ли?

— Ну конечно, потому что, кроме четных и нечетных, больше никаких нет. Так они и идут одно за другим: нечетное, потом четное, потом опять нечетное и так далее без конца.

— Одно за другим, по очереди?

— Конечно! Что ты меня спрашиваешь о таких вещах? Уж это, кажется, до того просто, что малое дитя знает!

— Ах, так это просто, по-твоему? Ну посмотрим, что ты дальше скажешь! Так, значит, выходит, что четных и нечетных чисел одинаковое количество.

— Конечно, — ответил Илюша. — Если взять, например, до какого-нибудь четного числа, ну хоть до этого нонильона децильонов, то будет поровну и четных и нечетных.

— Так и запишем. Попробуем только взять еще немножко подальше, а то для Мишкиной задачки это крохотное числишко — нонильон децильонов — не подходит. Возьмем до бесконечности. Так вот, ответь мне, пожалуйста: если мы возьмем все числа, а потом выберем только одни четные и напишем в два ряда — в одном ряду будут все: и четные и нечетные, а в другом одни четные, — так в котором ряду будет чисел больше, в верхнем или в нижнем?

— Ну конечно, во втором ряду будет вдвое…

Но тут почему-то Илюша замолчал, и на его лице изобразилось полнейшее недоумение.

— Ну-с, — сказал Радикс, — я вас слушаю! В котором ряду будет больше, в верхнем или в нижнем?

Илюша грустно вздохнул и сказал:

— Должно быть во втором ряду вдвое меньше, а на самом деле…

— А на самом деле? — повторил вопросительно Радикс. — Да что тут долго думать! Вон они, посмотри-ка!

Илюша обернулся, посмотрел на стену и увидел:

1 2 3 4 5 6 7 8 9 10 11 12 13 14…

2 4 6 8 10 12 14 16 18 20 22 24 26 28…

Оба ряда тянулись вправо ужасно далеко, но как ни заглядывал Илюша вправо, как он ни напрягал зрение, оба они шли совершенно вровень, а конца им не было.

— Так как же? — опять спросил Радикс.

— 208 —

— Выходит, что их — и тех и других — одно и то же количество.

Илюша пожал плечами.

— Не понимаю! — сказал он. — Вижу, что одно и то же количество, и соображаю, что сколько ни тяни верхний ряд, нижний от него отставать не будет, потому что нижний — это тот же верхний, только умноженный на два, но понять не могу.

Не могу, потому что нижний в то же самое время есть часть верхнего. Но ведь часть меньше своего целого?

— Меньше, покуда речь идет о числах, о конечных величинах. А раз ты имеешь дело с бесконечностью, то, как ты сейчас сам видишь, это не так. Там вовсе не обязательно, чтобы часть была меньше своего целого. В данном случае часть совершенно такая же, как и ее целое. И это странное целое можно еще по-разному разбить на части, и опять получится то же самое. Великий Галилео Галилей в книге, которая называется «Беседа о двух новых науках» и которая вышла в свет в тысяча шестьсот тридцать восьмом году, задает примерно такой вопрос: «Верно ли будет, если я скажу, что количество правильных квадратов, как «четыре», «девять», «шестнадцать», «двадцать пять» и так далее, меньше количества всех чисел, поскольку число правильных квадратов непрерывно и очень скоро убывает по мере того, как мы двигаемся вперед по натуральному ряду чисел по направлению ко все большим и большим числам? Для примера укажу, что в первой сотне я насчитываю десять квадратов, что составляет одну десятую всех чисел до сотни включительно; затем до десяти тысяч их будет сто, то есть одна сотая, а до миллиона их будет одна тысячная и так далее». Поскольку это так, то несомненно правильно, что в любом конечном числе квадратов будет гораздо меньше, чем всех чисел, и чем оно будет больше, тем относительно их будет меньше. Однако, как только мы переходим к бесконечности, оказывается, что я могу все это рассмотреть совершенно с другой точки зрения. Напишем вот таких два ряда:

1 2 3 4 5 6 7 8 9 10 11 12…

1 4 9 16 25 36 49 64 81 100 121 144…

Под каждым числом натурального ряда я подписываю во втором ряду его квадрат, и оба ряда будут тянуться вровень без конца. «Поэтому, — говорит далее Галилей, — нельзя сказать, которых чисел больше, которых меньше. Можно только сказать, что их бесконечное множество — и тех и других». Свойства конечных чисел, таким образом, на бесконечные множества распространять невозможно.

— 209 —

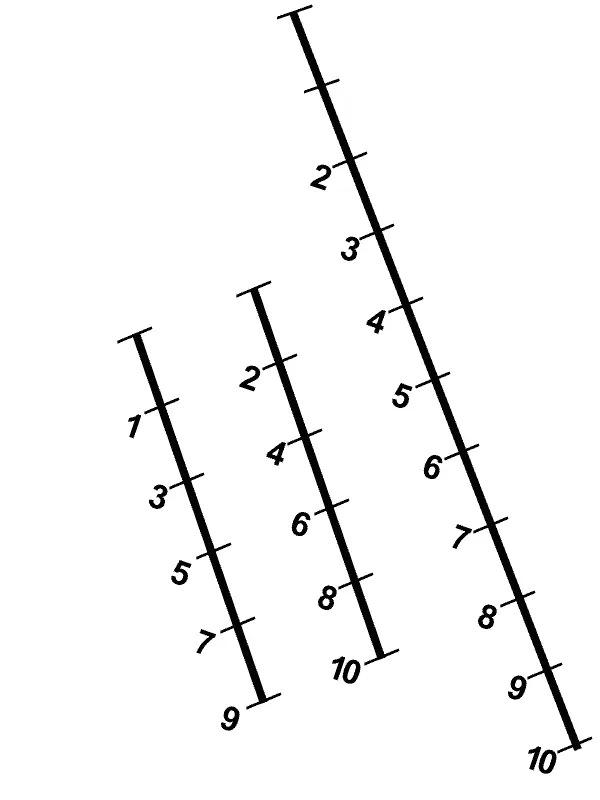
Из этого луча можно сделать два луча.

— Все это так, — медленно произнес Илюша, — а понять все-таки очень трудно.

— Ничего удивительного здесь нет, — отвечал Радикс, — что тебе вся эта задача кажется такой трудной. Современные ученые полагают, что она была настолько трудна для современников Галилея, что не столько привлекла их внимание к этим тонким вопросам, сколько отпугнула их своей необычностью и необъяснимостью. Но не торопись, кое-что можно будет тебе разъяснить в дальнейшем.

— Хорошо бы… — отвечал наш герой.

— Трудность здесь заключается в том, что мы не можем пересчитать числа в том и другом ряду. Так как это невозможно, то нам остается только подумать, нельзя ли найти какой-нибудь способ сравнивать друг с другом бесконечные множества. И вот что тут можно предложить. Представь себе, что ты пришел в школу на вечер. Собралась масса мальчиков и девочек. Зал большой, страшная толкотня, а тебе хочется узнать, кого больше: мальчиков или девочек? Сколько тех и других, тебя не интересует. Ты хочешь только выяснить, кого больше. Как это сделать? Самое простое — попросить оркестрантов, чтобы они заиграли вальс. Тотчас же все станут парами, и тут ты увидишь, кого больше. Теперь ты видишь, что я и применяю этот самый способ к бесконечным множествам, например ко множеству всех чисел и множеству квадратов: сопоставляю их попарно, а раз это удается, значит, что никакой разницы между множеством всех чисел и множеством квадратов в отношении количества их элементов нет.

— 210 —

Но только математики говорят в таких случаях не «количество» элементов, а так: эти два множества имеют «одинаковую мощность» [16] Наш дорогой читатель хорошо сделает, если постарается раздобыть книжку Н. Я. Виленкина «Рассказы о множествах», М., «Наука», 1965. Книжечка небольшая (128 стр.), не очень легкая, но одолеть ее вполне возможно. Там рассмотрены те же примеры, что и здесь приводятся, но есть и еще более интересные и сложные. .