Рене Декарт - Рассуждения о методе. Начала философии. Страсти души (сборник)

XXVII. А так как это происходило бы не от того действия, которое, по нашему пониманию, существует в движущемся или в прекращающем движение теле, но от одного перемещения и отсутствия перемещения (то есть покоя), то ясно, что это перемещение не может быть вне движущегося тела и что это тело находится в одном состоянии, когда переносится, и в ином, когда не переносится (то есть покоится); значит, движение и покой суть не что иное, как два различных модуса тела.

XXVIII. Сверх того я прибавил, что перемещение совершается из соседства одних соприкасающихся тел в соседство других, но не из одного места в другое; ведь, как я изложил выше, значения слова «место» различны и зависят от нашего мышления. Но когда под движением тела разумеется его перемещение из соседства соприкасающихся тел, то благодаря тому, что в данный момент времени только одни определенные тела могут соприкасаться с движимым телом, этому последнему возможно приписать одновременно только одно движение.

XXIX. Наконец, я прибавил, что такое перемещение совершается из соседства не всех каких угодно соприкасающихся тел, но только из соседства тех, которые рассматриваются как покоящиеся. Само же перемещение взаимно, и нельзя мыслить тела АВ переходящим из соседства с телом CD, не подразумевая вместе с тем перехода CD из соседства с АВ. Одни и те же сила и действие требуются как с той, так и с другой стороны. Поэтому, если мы хотим приписать движению особенную, только ему свойственную природу, то, в случае перемещения двух смежных тел, одного в одну сторону, другого в другую, благодаря чему тела как бы взаимно разделяются, мы скажем, что движение одинаково существует в обоих телах. Но это суждение слишком далеко отходит от обычного способа выражения. Привыкнув стоять на Земле и считать последнюю покоящейся, мы, если и видим, что отдельные ее части, смежные с иными мелкими телами, переходят из этого соседства, не считаем, однако, что сама Земля движется.

XXX. Главное основание этого убеждения состоит только в том, что движение мыслится присущим целому движущемуся телу, и, таким образом, не может мыслиться движение всей Земли, ввиду перенесения некоторых частей последней из соседства меньших тел, с которыми они соприкасаются, ибо часто наблюдаются на самой Земле многочисленные взаимно противоположные перемещения такого рода. Например, если тело EFGH (рис. 1) – Земля и на ней одновременно движутся: тело АВ от Е к F и тело CD от Н к G, то хотя тем самым части Земли, соприкасающиеся с телом АВ, переносятся от В к А и для их перемещения должно быть дано в них действие не меньшее и такой же природы, как в теле АВ, – мы однако не принимаем в расчет, что Земля движется от В к А, то есть с запада на восток. Ведь в таком случае из того, что части Земли, смежные с телом CD, переносятся от С к D, должно было бы с равным основанием заключать, что Земля движется в иную сторону, с востока на запад, а это были бы два противоположных движения. Следовательно, чтобы не отступать чрезмерно от обычного словоупотребления, мы не скажем здесь, что движется Земля, а будем говорить лишь о движении тел АВ и CD; так и в иных случаях. Но при этом мы будем помнить, что все реальное и положительное в движущихся телах, благодаря чему они и называются движущимися, находится также в других, соприкасающихся с первыми телах, хотя, однако, последние рассматриваются как покоящиеся.

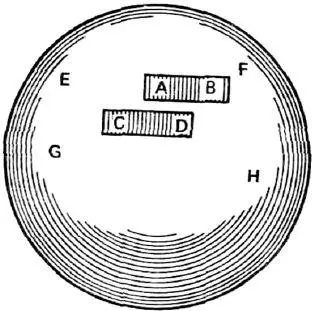
Рис. 1

XXXI. Хотя каждое тело имеет лишь одно свойственное ему движение, ибо понимается как удаляющееся только от одних соседних с ним и покоящихся тел, однако оно может принимать участие в других бесчисленных движениях, если, конечно, составляет часть иных тел, обладающих другими движениями. Так, если кто-нибудь, гуляя по кораблю, имеет в кармане часы, то колесики этих часов движутся так, как свойственно только им одним; но они причастны и еще иному движению, поскольку, будучи отнесены к гуляющему человеку, составляют одну с ним материальную массу; причастны они и второму движению, поскольку будут отнесены к плывущему по морю кораблю, – и третьему, поскольку будут отнесены к этому самому морю, и, наконец, четвертому, поскольку будут отнесены к самой Земле, если, конечно, вся Земля движется. Всеми этими движениями наши колесики действительно будут обладать; но ввиду трудности за раз мыслить столь многочисленные движения и ввиду того, что не все из них могут быть познаны, достаточно полагать в теле только одно движение, ближайшим образом ему принадлежащее.

XXXII. Кроме того, единое движение каждого тела, свойственное последнему, может быть рассматриваемо наподобие многих движений. Так, в колесах колесниц мы различаем два разных движения: одно – круговое, по оси, другое – продольное, по пути движения колесницы. Но что оба эти движения не различаются в действительности, ясно из того, что любая точка движущегося тела описывает лишь одну определенную линию. Не важно, что эта линия часто слишком запутанна и потому кажется результатом множества различных движений, ибо можно представить, что всякая, даже прямая линия, простейшая из всех, возникла из бесчисленных различных движений. Так, например, если линия АВ движется к CD и одновременно точка А приближается к В, то прямая, описываемая этой точкой А, зависит от двух прямых движений (А к В и АВ к CD) не менее, чем кривая линия, описываемая точкой колеса, зависит от А, прямого и кругового движения. Поэтому, хотя часто полезно разделять подобным образом одно движение на многие части, абсолютно говоря, каждому телу должно причитаться одно только движение.

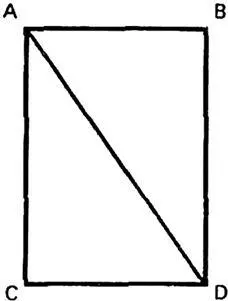
Рис. 2

XXXIII. Но, как замечено выше, все пространство заполнено телами и количество одних и тех же частиц материи в равных местах всегда равно; отсюда следует, что ни одно тело не может двигаться иначе как по кругу, то есть таким образом, что оно изгоняет какое-либо иное тело с того места, куда вступает, а это второе тело изгоняет третье, а это – четвертое, и так до последнего тела, вступающего на место, оставленное первым телом, в тот самый момент, когда место оставлено. Это легко мыслить в совершенном круге, ибо мы увидим, что там нет ни пустоты, ни сгущения или разрежения, когда частица круга А движется по направлению к В, в то время как частица В движется к С, С к D, а D к А (см. рис. 3). То же самое можно мыслить и в несовершенном и сколь угодно неправильном круге, раз замечено, при каких условиях все неровности мест могут возмещаться разницей в скорости движения. Так, вся материя, заключенная в пространстве EFGH (см. рис. 4), может кругообразно двигаться без сгущения или образования пустоты, и в то время как ее частица, направляющаяся к Е, переходит из G, та, которая направляется к G, переходит из Е; а переходят частицы таким образом, что если пространство в G предполагается вчетверо шире, чем в Е, и вдвое шире, чем в F и Н, то частица движется в Е с учетверенной скоростью относительно скорости в G и с удвоенной скоростью относительно скорости в F и Н. Следовательно, при прочих равных условиях, быстрота движения возмещает узость места. При этом условии в любое определенное время через каждую из частей этого круга проходит одинаковое количество материи.