Карл Зигмунд - Точное мышление в безумные времена. Венский кружок и крестовый поход за основаниями науки

Вскоре было показано, что вдобавок к гёделевскому утверждению G , которое при помощи нумерации Гёделя истинно утверждает: «Меня нельзя доказать», существует бесконечно много других истинных утверждений, которые нельзя доказать, зато они выглядят гораздо привычнее для математиков — например, существуют недоказуемые истинные утверждения, по форме схожие с гипотезой Гольдбаха, которую Гёдель упоминал на съезде в Кенигсберге. Это весьма поучительный пример.

Еще в 1742 году математик-любитель Кристиан Гольдбах предположил, что любое четное число больше 2 представляет собой сумму двух простых чисел. Отчасти это можно проверить. Так, 6 = 3 + 3, 12 = 5 + 7 и т. д. Самые быстрые компьютеры на Земле позволили проверить гипотезу Гольдбаха для всех четных чисел до 300 000 000 000 000 000 (17 нулей). Это виртуозное достижение, естественно, не доказывает гипотезу Гольдбаха и даже не приближает нас к доказательству: ведь по-прежнему остается бесконечно много четных чисел, до проверки которых еще не дошла очередь!

Компьютерная программа способна исследовать каждое четное число и проверять, представляют ли они собой сумму двух простых чисел. Если гипотеза Гольдбаха ошибочна, компьютер когда-нибудь это покажет, надо просто подождать, пока он доберется до четного числа, которое не будет представлять собой сумму двух простых чисел. Но если гипотеза верна, компьютер будет трудиться бесконечно, а нам придется до второго пришествия сидеть и ждать, не зная, найдется ли когда-нибудь исключение. Очевидно, гипотезу Гольдбаха так не докажешь. Компьютерная программа может подтвердить ложность гипотезы (если она и в самом деле ложна), поскольку это займет лишь конечное время, но не может подтвердить ее истинность (если она в действительности истинна), поскольку на это требуется бесконечное время.

Подобным же образом компьютер способен проинспектировать любую формальную математическую последовательность формул, ведь такая последовательность — всего лишь цепочка символов, и проверить, есть ли у нее формальное доказательство. Такая проверка — акт сугубо механический, и он не требует понимания, что означают те или иные символы. Компьютер может проинспектировать все возможные подобные тексты по одному, стоящие в бесконечном списке по возрастанию длины. Этот список никогда не исчерпать. Но если можно доказать либо утверждение А , либо его отрицание не- А , тогда компьютер обязательно найдет соответствующее доказательство: оно ведь есть где-то в этом списке.

Поначалу представляется, будто из всего этого следует, что все математические утверждения можно механически рассортировать. Запустите компьютер и поглядите, что он найдет первым — доказательство А или доказательство не- А . Пара пустяков!

Но тут есть загвоздка, которая в том и состоит, что благодаря теореме Гёделя о неполноте существуют истинные утверждения, для которых нет формального доказательства. Если А принадлежит к таким формулам, то компьютер будет продолжать процесс проверки бесконечно и так никогда и не определит, ложно или истинно А , ведь ни у А , ни у его отрицания нет доказательства!

Таким образом, теорема Гёделя о неполноте предвосхищает важнейшие идеи об абсолютных пределах возможностей компьютерных программ. Первым до них докопался английский математик Алан Тьюринг (1912–1954) в 1936 году. С годами Гёделю, Тьюрингу и другим гениальным логикам удалось установить, что процесс математического мышления невозможно полностью свести к чисто формальным аксиоматическим рассуждениям. В этом смысле математика — неисчерпаемый источник.

Через несколько десятков лет после прорывных статей Гёделя и Тьюринга в мире завоевала невероятную популярность логическая игра судоку — ей увлекались миллионы. Это показывает, что логика может быть очень интересной. Более того, головоломки судоку можно считать аналогичными формальным математическим теориям à la Гильберт, и сейчас мы в этом убедимся.

Цель игры в судоку — расставить цифры от 1 до 9 в 81 ячейке в квадрате 9 × 9 так, чтобы каждая цифра встречалась в каждом ряду, в каждом столбце и в каждом мини-квадрате 3 × 3 только один раз.

В нескольких ячейках цифры уже расставлены, что называется, бонусом. Так вот, в нашей аналогии с формальными системами заранее заданные цифры — это «аксиомы». Мы ждем, что нормальная головоломка судоку, во-первых, имеет решение, во-вторых, это решение единственное. То есть предполагается, что для каждой из 81 ячейки найдется одна и только одна цифра, удовлетворяющая условиям. Если найдется какая-то ячейка, которую в принципе нельзя заполнить, значит, «аксиомы» ведут к противоречию. А если есть ячейка, которую можно заполнить двумя и более разными способами, значит, «аксиомы» неполны: задача о том, какие цифры подходят в какие ячейки, не имеет решения. Нужны дополнительные «аксиомы», чтобы задать единственно верное расположение цифр. То есть идеальная головоломка судоку должна быть одновременно и полной, и непротиворечивой.

Однако ждать того же от формальной системы математики — значит неизбежно разочароваться. Именно это Гёдель и показал в 1931 году. Впоследствии Людвиг Витгенштейн подвел под этим черту следующим образом: «Теорема Гёделя вынуждает нас рассматривать математику под новым углом» [312] 312 Wittgenstein MS 163 (Рукопись № 163 по каталогу G. H. von Wright), July 11, 1941, см. Nedo, 2012, 378. . (Впрочем, большинство исследователей сходятся на том, что ни Витгенштейн, ни Рассел на самом деле не понимали идей Гёделя.) Теперь, когда мы прекрасно знаем, как все обстоит на самом деле, сама мысль, что все истинные утверждения математики (но не ложные) можно выявить по одному благодаря трудолюбивой компьютерной программе, выглядит так же диковинно, как надежды алхимиков обрести философский камень. Нельзя заменить живых математиков холодными строгими автоматами. Вероятно, так можно сказать и о других профессиях, но этого никто не доказал. (И в качестве реплики в сторону: в 2013 году математик Харальд Хельфготт доказал, что любое нечетное число представляет собой сумму трех простых чисел. Тем не менее мы ни на волосок не приблизились к доказательству гипотезы Гольдбаха.)

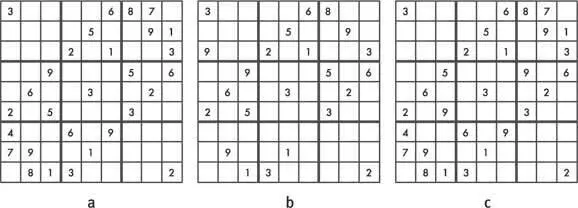
Примеры судоку: (а) неполное, (b) противоречивое, (c) «нормальное»

Гёделя иногда понимают неправильно. Разумеется, это практически неизбежно, и эту участь Гёдель разделяет с Дарвином и Эйнштейном и другими великими первопроходцами в науке. Кто-то утверждает, что Гёдель доказал, что математика противоречива. Это вовсе не так. Он доказал, что ее непротиворечивость невозможно формально доказать. Примерно так же вам, вероятно, не удастся обеспечить стопроцентно убедительное юридическое доказательство, что вы никогда в жизни не совершали убийства, — ни разу. Несмотря на это, мы, как правило, изначально не считаем никого убийцей. Так же и с математикой. Никто всерьез не верит, что математика внутренне противоречива. Перефразируя слова одного французского математика, изящно сформулировавшего девиз своей профессии, «Бог создал математику непротиворечивой, а дьявол сделал так, чтобы это нельзя было доказать».