Георг Гегель - Наука логики. Том I. Объективная логика

Но выражение, которое бесконечность находит в изображении ее числовой дробью, еще несовершенно потому, что оба члена дроби, 2 и 7, могут быть изъяты из отношения, и тогда они суть обыкновенные безразличные определенные количества; их соотношение, то обстоятельство, что они суть члены отношения и моменты, есть для них нечто внешнее и безразличное. И точно так же само их соотношение есть обыкновенное определенное количество, показатель отношения.

Буквам , которыми оперируют в общей арифметике, т. е. ближайшей всеобщности, в которую возводятся числа, не присуще свойство обладать определенной числовой величиной; они суть лишь всеобщие знаки и неопределенные возможности любой определенной величины. Дробь 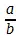представляется поэтому более подходящим выражением бесконечного, так как a и b , изъятые из их взаимоотношения, остаются неопределенными и не обладают особой им принадлежащей величиной, даже будучи отделены друг от друга. — Однако, хотя эти буквы положены как неопределенные величины, их смысл все же состоит в том, что они суть какое-либо конечное определенное количество. Так как они суть хотя и всеобщее представление, но лишь об определенном числе , то для них равным образом безразлично то обстоятельство, что они находятся в отношении, и вне последнего они сохраняют то же самое значение.

Если присмотримся еще ближе к тому, что представляет собою отношение, то мы увидим, что ему присущи оба определения: оно, во-первых , есть некоторое определенное количество, но последнее есть, во-вторых , не некоторое непосредственное, а определенное количество, содержащее в себе качественную противоположность; оно вместе с тем остается в отношении тем данным, безразличным определенным количеством благодаря тому, что оно возвращается из своего инобытия, из противоположности, в себя, и, следовательно, есть также некоторое бесконечное. Эти два определения, развитые в их отличии друг от друга, представляются в следующей общеизвестной форме.

Дробь 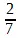может быть выражена как 0,285714..., 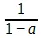, — как 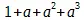и т. д. Таким образом, она имеет бытие как некоторый бесконечный ряд ; сама дробь называется суммой или конечным выражением этого ряда. Если сравним между собою эти два выражения, то окажется, что одно, бесконечный ряд, уже представляет ее не как отношение, а с той стороны, что она есть некоторое определенное количество как множество таких количеств, которые присоединяются одно к другому, — как некоторая численность. — Что величины, долженствующие ее составить как некоторую численность, сами в свою очередь состоят из десятичных дробей, сами, следовательно, состоят из отношений, это здесь не имеет значения; ибо это обстоятельство касается особого рода единицы этих величин, а не их, поскольку они конституируют численность ; ведь и состоящее из нескольких цифр целое число десятеричной системы также считается по существу одной численностью и не обращается внимания на то, что она состоит из произведений некоторых чисел на число десять и его степени. Равным образом здесь не имеет значения то обстоятельство, что имеются другие дроби, нежели взятая в виде примера дробь 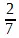, которые, будучи обращены в десятичные дроби, не дают бесконечного ряда; однако каждая из них может быть изображена как таковой ряд в числовой системе другой единицы.

Так как в бесконечном ряде, который должен представлять собою дробь как некоторую численность, исчезает тот аспект, что она есть отношение, то исчезает также и тот аспект, что она, как мы показали выше, имеет бесконечность в ней (в дроби). Но эта бесконечность вошла другим образом, а именно, сам ряд бесконечен.

Какого рода эта бесконечность ряда, явствует само собою; это — дурная бесконечность прогресса. Ряд содержит в себе и представляет собою то противоречие, что нечто, являющееся отношением и имеющее внутри себя качественную природу, изображается как лишенное отношений, как исключительно только определенное количество , как численность. Следствием этого противоречия оказывается то, что в численности, выражаемой в ряде, всегда чего-то недостает, так что всегда нужно выходить за пределы того, что положено, чтобы достигнуть требуемой определенности. Закон этого поступательного движения известен; он заключается в определении определенного количества, содержащегося в дроби, и в природе формы, в которой это определение должно быть выражено. Можно, правда, посредством продолжения ряда сделать численность столь точной, сколь это нужно . Однако изображение численности посредством ряда всегда остается лишь долженствованием ; оно обременено некоторым потусторонним , которое не может быть устранено, так как выражение в виде численности того, что основано на качественной определенности, представляет собою постоянное противоречие .

В этом бесконечном ряде действительно имеется та неточность , которая в истинном математическом бесконечном встречается лишь как видимость. Не следует смешивать эти два вида математического бесконечного, точно так же, как не следует смешивать вышеуказанные два вида философского бесконечного. Первоначально применяли для изображения истинного математического бесконечного форму ряда , и в новейшее время она опять была вызвана к жизни. Но она для него не необходима. Напротив, как сделается ясным в дальнейшем, бесконечное бесконечного ряда существенно отлично от этого истинного бесконечного. Он, напротив, уступает в этом отношении даже выражению бесконечного, даваемому дробью.

А именно, бесконечный ряд содержит в себе дурную бесконечность, так как то, что должно быть выражено рядом, остается долженствованием , а то, что он выражает, обременено неисчезающим потусторонним и отлично от того, что должно быть выражено. Он бесконечен не из-за тех своих членов, которые положены, а потому, что они неполны, так как другое, которое по существу принадлежит к ним, находится по ту сторону их; то, что в нем есть, хотя бы положенных членов было сколь угодно много, есть лишь конечное в собственном смысле этого слова, положено как конечное, т. е. как нечто такое, что не есть то, чем оно должно быть . Напротив, то, что называется конечным выражением или суммой такого ряда, безупречно; оно содержит в себе полностью то значение, которого ряд только ищет; убегавшее потустороннее снова возвращено назад; то, что этот ряд есть, и то, чем он должен быть, уже не разделено, а есть одно и то же.