Валентин Асмус - ЛОГИКА

§ 18. Частноутвердительное суждение даёт при обращении частноутвердительное суждение — при условии, если субъект и предикат — понятия перекрещивающиеся. Если же предикат подчинён субъекту, то частноутвердительное суждение обращается в общеутвердителъно е.

Рассмотрим сначала обращение частноутвердительного суждения, в котором субъект и предикат — понятия перекрещивающиеся. Таково, например, суждение: «некоторые учёные — публицисты» (I). Суждение это даёт при обращении частноутвердительное суждение: «некоторые публицисты —учёные» (I). Правило это выводится из распределённости понятий в обращаемом суждении. В суждении этом не распределены ни субъект, ни предикат. То, что некоторые учёные составляют часть класса публицистов, конечно, ещё не означает, что этими некоторыми учёными исчерпывается весь объём предиката, т. е. весь класс публицистов: публицист не необходимо должен быть учёным. Так как в обращаемом суждении предикат мыслится не во всём объёме, то в обращённом суждении, где предикат этот становится субъектом, речь также не может итти о всём объёме этого субъекта. Но это и значит, что из частноутвердительного суждения этого типа при обращении должно получиться также частноутвердительное суждение.

Легко выводимое из условий распределённости субъекта и предиката правило это в свою очередь опирается на отношения между содержанием понятия субъекта и содержанием понятия предиката. И действительно: обращение возможно здесь лишь потому, что «некоторые публицисты», понятие которых мыслится в предикате обращаемого суждения, — это именно те «некоторые учёные», понятие которых мыслится в субъекте обращаемого суждения. Равны же объёмы этих двух понятий только потому, что тождественны их содержания: признаки той части публицистов, которая мыслится в предикате обращаемого суждения, — те же самые, что признаки той части учёных, которая мыслится в субъекте обращаемого суждения (см. рис. 25).

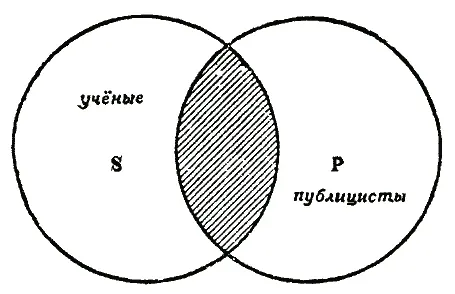
Рис. 25

Из рисунка видно, что заштрихованная часть объёма понятия «учёные», представленного кругом S, совпадает с частью объёма понятия «публицисты», представленного кругом Р. Это значит, что часть учёных являются публицистами. Именно это отношение тождества между частью объёма понятия «учёные» и частью объёма понятия «публицисты» мыслится в исходной — необращённой — форме суждения.

Но из этого же рисунка видно, что и наоборот: часть объёма понятия «публицисты» совпадает с частью объёма понятия «учёные». Это значит, что часть публицистов является учёными. Именно это отношение тождества между частью объёма понятия «публицисты» и частью объёма понятия «учёные» мыслится в обращённом суждении: «некоторые публицисты —учёные».

Рассмотрим теперь обращение частноутвердительного суждения, в котором предикат подчинён субъекту. Таково, например, суждение: «некоторые писатели — драматурги» (I). Суждение это даёт при обращении общеутвердительное суждение: «все драматурги — писатели» (А). Обращение это выводится из распределённости терминов в обращаемом суждении. В суждении этом понятие субъекта («некоторые писатели») не распределено, но понятие предиката («драматурги») распределено (см. рис. 26).

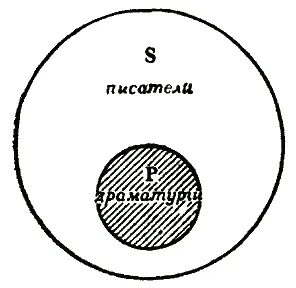
Рис. 26

Как видно из рисунка, к объёму драматургов (Р) принадлежит не весь объём писателей (S), но лишь часть этого объёма. Это — та часть объёма S, которая совпадает с объёмом Р и которая заштрихована на рисунке. Но этой частью объёма S, принадлежащей объёму Р, объём Р исчерпывается полностью: весь объём драматургов входит в объём писателей. Поэтому в обращённом суждении мыслятся не «некоторые драматурги», но «все драматурги».

Нетрудно убедиться, что отношение между объёмами субъекта и предиката, мыслимое в суждениях этого типа, основывается, как всегда, на отношении между содержанием субъекта и содержанием предиката. Так как все существенные признаки, составляющие содержание понятия «писатели», входят как часть в содержание понятия «драматурги», то весь объём понятия «драматурги» составляет часть объёма понятия «писатели».

§ 19. Общеотрицательное суждение даёт при обращении также общеотрицательное суждение. Так, суждение «ни одна планета не есть звезда» (Е) обращается в суждение «ни одна звезда не есть планета». Правило это следует из распределённости понятий в общеотрицательных суждениях. В таком суждении распределены и субъект и предикат. Во-первых, высказывание относится в нём ко всему объёму субъекта ; ни о какой части объёма планет нельзя сказать, что она есть часть объёма звёзд. Во-вторых, высказывание относится и ко всему объёму предиката . Суждение «ни одна планета не есть звезда» означает, что весь логический класс звёзд не заключает ни в какой части своего объёма светил, называемых планетами.

Отсюда легко выводится правило обращения общеотрицательных суждений: так как предикат обращаемого суждения мыслится во всём своём объёме, то и при обращении, где предикат этот становится субъектом , он будет мыслиться во всём своём объёме, т. е. обращённое суждение окажется общим . Но оно окажется также и отрицательным .

И действительно: обращаемое суждение удостоверяет, что весь объём планет находится целиком вне всего объёма звёзд. Но это значит, что и наоборот: весь объём звёзд находится целиком вне всего объёма планет.

Выводимое из условий распределённости понятий правило обращения общеотрицательных суждений в свою очередь выводится из отношения содержания субъекта к содержанию предиката в общеотрицательных суждениях. В суждениях этих весь объём предиката находится вне всего объёма субъекта только потому, что субъект и предикат — несовместимые понятия. Так, например, объём понятия «звёзды» находится вне объёма понятия «планеты». Именно в силу этой несовместимости данных понятий ни планеты не могут входить в число звёзд, ни, обратно, звёзды — в число планет (см. рис. 27).

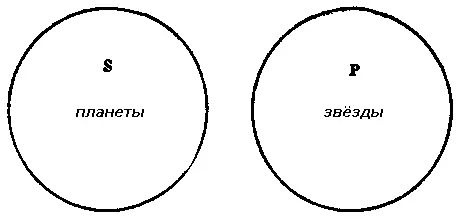
Рис. 27

Из рисунка видно, что ни одна часть объёма понятия «планеты», представленного кругом S, не совпадает ни с одной частью объёма понятия «звёзды», представленного кругом Р. Именно это отношение между понятиями S и Р мыслится в исходной — необращённой — форме суждения: «ни одно S не есть Р».