Валентин Асмус - ЛОГИКА

§ 25. Общеотрицательное суждение преобразуется посредством противопоставления предикату в частноутвердительное суждение. Рассмотрим, например, суждение «ни один паук не есть насекомое». Какое высказывание может быть получено из него относительно «не-насекомых»? Очевидно, таким высказыванием будет: «некоторые не-насекомые — пауки». И действительно, преобразуемое суждение устанавливает, что внутри логического класса «насекомых» не может быть ни одной части логического класса «пауков». Но это значит, что из числа животных, которые не являются насекомыми, некоторые принадлежат к паукам (см. рис. 31).

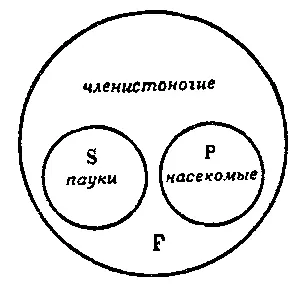
Рис. 31

На этом рисунке круг F представляет весь объём логического класса членистоногих, куда входят как соподчинённые ему объёмы логического класса «пауков» (S) и логического класса «насекомых»(Р).

Из рисунка видно, что ни один паук не есть насекомое. Именно этот смысл выражает суждение до преобразования. На этом же рисунке «не-насекомые» представлены всей той частью круга F, которая находится вне круга Р. Из рисунка видно, что некоторые не-Р будут S, т. е. что некоторые из этих не-насекомых будут пауками. Именно это выражает та форма суждения, которая получается в результате преобразования посредством противопоставления предикату.

§ 26. Частноотрицательное суждение преобразуется посредством противопоставления предикату в частноутвердительное суждение. Рассмотрим, например, частноотрицательное суждение «некоторые летательные машины не принадлежат к числу самолётов». Зададимся вопросом: какое высказывание может быть получено из него относительно понятия, противоречащего предикату? Так как предикатом суждения является понятие «самолёты», то противоречащим ему понятием будет, очевидно, понятие «не-самолёты».Что же можно высказать об этом понятии? Очевидно то, что «некоторые не-самолёты принадлежат к числу летательных машин» (см. рис. 32).

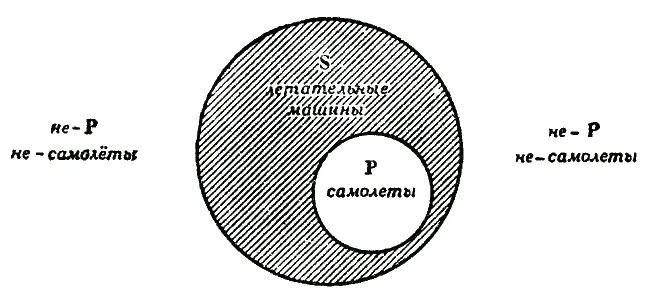
Рис. 32

Из рисунка видно, что объём самолётов (круг Р) составляет часть объёма летательных машин (круг S). Этот же рисунок показывает, что некоторые летательные машины не принадлежат к числу самолётов. Именно этот смысл выражает форма суждения до преобразования. Часть объёма летательных машин, которая не принадлежит к объёму самолётов, представлена на рисунке заштрихованной частью круга S, т. е. частью круга S, лежащей вне круга Р.

Этот же рисунок показывает, что объём не-самолётов, как объём всякого противоречащего понятия, изображается всей неопределённо простирающейся во все стороны вне круга Р плоскостью.

Из рисунка видно, что в состав этой плоскости входит заштрихованная часть плоскости круга S, лежащая вне круга Р. Но именно это и выражает форма суждения, получившаяся в результате преобразования посредством противопоставления предикату: «некоторые не-самолёты принадлежат к числу летательных машин». Общая форма таких суждений: «некоторые не-Р принадлежат к S».

§ 27.Нетрудно убедиться, что каждое из полученных правил преобразования суждений посредством противопоставления предикату соответствует определённому правилу обращения. При обращении, например, общеутвердительного суждения получается частноутвердительное суждение. Преобразованию посредством противопоставления предикату, очевидно, соответствует преобразование общеотрицательного суждения в частноутвердительное.

И точно так же правилу, по которому частноотрицательное суждение обычно не обращается, очевидно, соответствует правило о том, что при преобразовании посредством противопоставления предикату частноутвердительное суждение обычно не преобразуется.

В том, что существует соответствие между правилами обращения и правилами преобразования посредством противопоставления предикату, нет ничего удивительного. И действительно: при преобразовании посредством противопоставления предикату всегда получается высказывание относительно понятия, противоречащего предикату. Отсюда ясно, что каждому случаю обращения должен соответствовать некоторый определённый случай преобразования посредством противопоставления предикату.

Противопоставление предикату является соединением превращения с обращением. Чтобы произвести противопоставление, сначала производится превращение, а затем превращённое суждение обращается.

§ 28.Рассматривая превращение, мы ясно видим, что при операциях над суждением наша мысль, так же как и при операциях над понятием и выводом, опирается на законы тождества, противоречия, исключённого третьего и достаточного основания.

Согласно закону тождества, понятие предмета мыслится в исходной форме суждения как обладающее определённым признаком или отношением. Согласно закону противоречия, в превращённой форме суждения мыслится, что этот определённый признак или отношение, которые принадлежат понятию предмета, несовместимы с противоречащими им признаками или отношениями. Согласно закону исключённого третьего, в превращённой форме суждения мыслится, что между понятием об определённом признаке или отношении предмета и понятием, противоречащим ему, не существует никакого третьего понятия о признаке или об отношении, которое могло бы приписываться понятию предмета. Наконец, согласно закону достаточного основания, для превращения формы суждения необходимо достаточное основание. Таким основанием является мыслимое в исходной форме суждения отношение между понятием субъекта данного суждения и понятием его предиката.

1.Следующим суждениям придайте форму, удобную для логического анализа: «на вкус и на цвет товарища нет»; «пофилософствуй — ум вскружится» ( Грибоедов ); «когда в товарищах согласья нет, на лад их дело не пойдет» ( Крылов ); «гений и злодейство — две вещи несовместные» ( Пушкин ); «пойдёшь налево — коня потеряешь, пойдёшь направо — сам пропадёшь».

2.Определите, какие из следующих суждений являются общими и какие единичными: «все тела существуют в пространстве»; «все кредитные билеты составляют сумму в тысячу рублей»; «все кредитные билеты печатаются на бумаге с водяными знаками»; «рабочие заняли свои места у станков»; «рабочие — передовой класс буржуазного общества»; «знание — сила»; «тюрки — народ поэтов»; «жизнь есть форма существования белковых тел»; «круг делится диаметром на две равные части»; «планеты движутся вокруг солнца по эллипсам»; «общая масса всех планет составляет одну семисотую часть массы солнца».