Франсуа Шмитц - Витгенштейн [litres]

В целях упрощения рассмотрим только два возможных положения вещей, α и β, отображенные соответственно двумя элементарными предложениями – p и q. Напомним, что простые положения вещей являются взаимно независимыми, то есть существование или несуществование одного простого положения вещей совершенно не зависит от существования или несуществования другого простого положения вещей. Поэтому α и β могут сочетаться ни много ни мало четырьмя разными способами. Если мы условимся обозначать α тот факт, что α не существует, у нас получится четыре возможных сочетания: {<���α, β>, <���α, β>, < α, β>, < α, β>} (при наличии 3 положений вещей получилось бы соответственно 8 возможных сочетаний, и т. д.).

Итак, можно сказать, что форма возможной сложной ситуации, состоящая из двух положений вещей α и β, является совокупностью четырех возможных сочетаний, так же как и форма возможного положения вещей является совокупностью способов, которыми сочетаются простые объекты, составляющие его. Легко установить, что оба элементарных предложения p и q, если принимать во внимание исключительно их истинность или ложность, также могут сочетаться лишь четырьмя разными способами; если мы условимся обозначать p vтот факт, что p является истинным, а p f– тот факт, что p является ложным, у нас получится: {< p v, q v>,

v, q f>, < p f, q v>,

f, q f>}; таким образом эти четыре возможности элементарных предложений быть истинными или ложными соответствуют четырем возможностям положений вещей α и β быть существующими или несуществующими.

О чем говорит элементарное предложение? О том, что положение вещей, которое оно отображает, является существующим. О чем говорит молекулярное предложение, состоящее из p и q? О том, что некоторые, все или ни одно из четырех сочетаний {<���α, β>, <���α, β>, < α, β>, < α, β>} не являются существующими. Например, p или q говорит, что α и β являются существующими, или что α является существующим, или что β является существующим, и исключает то, что ни α, ни β не являются существующими. Другими словами, с одной стороны, это предложение выражает согласие с тремя первыми возможностями <���α, β>, <���α, β>, < α, β>, с другой – несогласие с возможностью < α, β>. Следовательно, в отличие от элементарного предложения, которое является истинным только при условии, что отображаемое им положение вещей является существующим, молекулярное предложение типа p или q является истинным только при условии, что одно из трех возможных сочетаний <���α, β >, <���α, β> или < α, β >является существующим. Таким образом, «условия истинности» p или q состоят в том, что p и q являются одновременно истинными, или в том, что p является истинным, или, наконец, что q является истинным.

До этого мы признавали, что знаем значение связки «и», для понимания которого одной записи p или q недостаточно. Тем не менее легко определить это значение с помощью следующей символики:

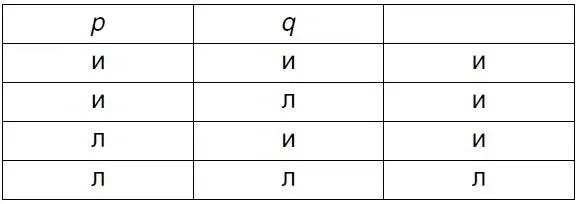
Буква «и» означает «истинное», буква «л» – «ложное», а правый столбец указывает, с какими «истинностными возможностями» p и q согласуется молекулярное предложение. Истинностные возможности, с которыми предложение согласуется, Витгенштейн называет основаниями истинности этого предложения. Таким образом, в правом столбце указано, каковы основания истинности молекулярного предложения. Здесь мы имеем дело с пропозициональным знаком, в котором слово «и» больше не присутствует и достоинством которого является то, что он прямо показывает, каковы условия истинности молекулярного предложения. Запомнив порядок расположения истинностных возможностей p и q , мы сможем записать это предложение еще более кратко, в доступном для понимания виде: (v, v, v, f) ( p, q ).

Наличие «множественности» у данного пропозиционального знака зависит от того, насколько точно соответствуют истинностные возможности предложения возможностям существования или несуществования положений вещей, отображаемых элементарными предложениями. Следовательно, пропозициональный знак не может согласовываться с одной (или несколькими) истинностной возможностью элементарных предложений, которые не соответствовали бы возможности существования или несуществования положений вещей, отображенных элементарными предложениями. Напротив, мы видели, как предложение « в 22 часа 30 минут у Жана была температура 37,5, и в 22 часа 30 минут у Жана была температура 39 градусов » согласовывалось с иллюзорной возможностью существования положений вещей: соединению элементарных предложений не соответствует ни одна возможность существования положений вещей, изображенных посредством этих двух элементарных предложений.

В более общем плане пропозициональный знак отражает, с каким подмножеством множества истинностных возможностей элементарных предложений он согласуется. Это замечание позволяет нам продвинуться дальше и выявить множество молекулярных предложений, состоящих из двух элементарных предложений, поскольку данное множество является лишь множеством подмножеств множества из четырех элементов {< p v, q v>,

v, q f>, < p f, q v>,

f, q f>}, которое соответствует множеству {<���α, β >, <���α, β >,< α,β>, < α, β>}. Так как множество из четырех элементов имеет шестнадцать (2 4) подмножеств, можно составить следующую таблицу:

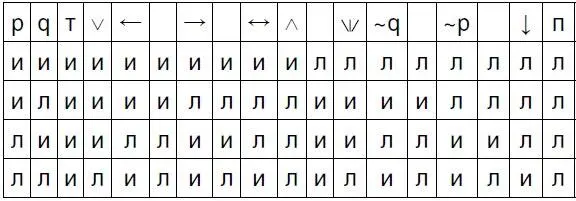
Небольшие символы, написанные в верхней части некоторых столбцов, обозначают логические союзы:

– p ˅ q соответствует p или q (инклюзивная дизъюнкция: оба элементарных предложения могут быть истинными);

– р ← q соответствует р если q;

– р → q соответствует если р, то q (импликация);

– р ↔ q соответствует если, и только если р, то q (двойная импликация);

– р ˄ q соответствует р и q (конъюнкция);

– р 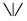q соответствует или р, или q (эксклюзивная дизъюнкция: два элементарных предложения не могут быть одновременно истинными);

– ~q (~p) соответствует не q (не р );

– р ↓ q соответствует ни р, ни q (инверсия).

Буквы «т» и «п» в верхней части двух столбцов обозначают два особых случая, которые мы вскоре рассмотрим, а именно «тавтологию» и «противоречие».